



Next: L'utilizzo degli Heap di
Up: Gli Heap di Fibonacci
Previous: Operazioni - Cancellazione di
Indice
Affinchè il costo ammortizzato della fuzione DECREASE-KEY e DELETE sia
realmente 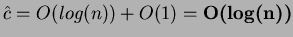 , dobbiamo dimostrare che il limite superiore al grado di
un qualsiasi nodo di uno Heap di Fibonacci è
, dobbiamo dimostrare che il limite superiore al grado di
un qualsiasi nodo di uno Heap di Fibonacci è 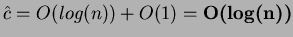 .
.
Chiameremo x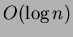 size il numero di nodi dell'albero
radicato in x (compreso x stesso). La dimostrazione mostra
anche come x
size il numero di nodi dell'albero
radicato in x (compreso x stesso). La dimostrazione mostra
anche come x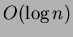 size è esponenziale a
x
size è esponenziale a
x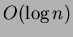 grado.
grado.
Lemma 1
Sia
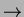
un nodo di un qualsiasi Heap di Fibonacci tale che abbia
(x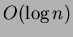 grado)
grado)=k. Siano
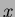
i suoi figli
ordinati in base al loro ordine di arrivo. Allora vale che
(
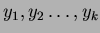 grado
grado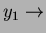
e (
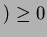 grado
grado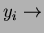
per i =
2,3,
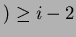
k.
Dimostrazione:
per dire che (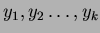 grado
grado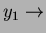 non serve dimostrazione; dato
non serve dimostrazione; dato
 si nota che quando
si nota che quando 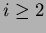 è diventato figlio di
è diventato figlio di  ,
,  aveva
i figli
aveva
i figli
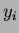 e quindi (
e quindi ( grado
grado ;
poichè
;
poichè 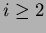 può essere stato aggiunto solo se aveva grado uguale a
può essere stato aggiunto solo se aveva grado uguale a
 , in quel momento si aveva (
, in quel momento si aveva (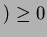 grado
grado .
Da quell'istante
.
Da quell'istante 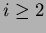 a perso al più un figlio perchè altrimenti
sarebbe stato tagliato (vedi sottosezione 2.8 ed in particolare la
funzione taglio-a-cascata). Ne consegue che (
a perso al più un figlio perchè altrimenti
sarebbe stato tagliato (vedi sottosezione 2.8 ed in particolare la
funzione taglio-a-cascata). Ne consegue che (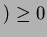 grado
grado
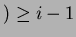
Con quello che stiamo per vedere si capisce finalmente perchè questo tipo
di struttura si chiami ``Heap di Fibonacci''. Come tutti sanno l'
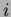 -esimo numero di Fibonacci è:
-esimo numero di Fibonacci è:
Il seguente lemma dimostra che 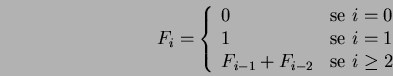 può essere espresso in un'altro modo:
può essere espresso in un'altro modo:
Lemma 2
per tutti gli
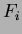
si possono esprimere i numeri di
Fibonacci come segue:
Dimostrazione:
Per induzione su 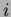 :
:
Per 
Data l'ipotesi induttiva
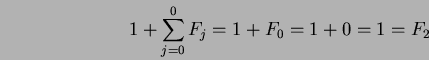 ,
si ha:
,
si ha:
Indichiamo con 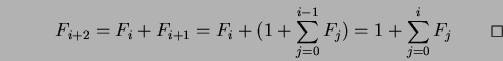 il cosiddetto rapporto aureo definito come
il cosiddetto rapporto aureo definito come
Il Lemma 4 che termina la dimostrazione utilizza il seguente
Lemma 3.
Dimostrazione(per induzione su 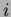 ):
):
Caso Base:
Semplice verifica per  e
e 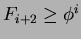
Passo Induttivo:
per ipotesi
basta quindi dimostrare che
cioè che
ed infatti sostituendo il valore di 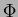 si verifica che
si verifica che
Lemma 4
sia
un nodo di uno Heap di Fibonacci e

. Allora vale che
dove
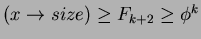
.
Dimostrazione:
Definiamo 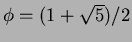 il minimo valore possibile di
il minimo valore possibile di 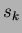 tra i nodi
tra i nodi
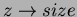 t.c.
t.c.
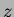 . Chiaramente si ha che
. Chiaramente si ha che 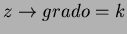 e
e
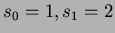 .
.
Dato un nodo  , siano
, siano
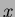 i suoi figli
ordinati in base al loro ordine di arrivo. Troviamo ora un limite
inferiore su
i suoi figli
ordinati in base al loro ordine di arrivo. Troviamo ora un limite
inferiore su 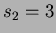 : sommiamo
: sommiamo 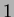 per
per  stesso,
stesso, 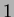 per il
primo figlio
per il
primo figlio 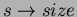 e poi
applichiamo via via il Lemma 1 per gli altri figli. Si ha quindi:
e poi
applichiamo via via il Lemma 1 per gli altri figli. Si ha quindi:
Resta ora da dimostrare per induzione su 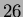 che
che
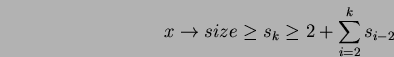 .
I casi di base (per
.
I casi di base (per 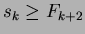 e
e  ) sono di verifica immediata.
) sono di verifica immediata.
Con  si prenda come ipotesi induttiva che
si prenda come ipotesi induttiva che
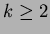 per
per
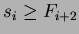 .
.
Abbiamo quindi:
Abbiamo quindi dimostrato che:
dove l'ultima disuguaglianza è data dal Lemma 3.
Con il Corollario 5 termina la parte relativa alla limitazione
del grado massimo.
Corollario 5
Il grado massimo
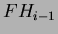
di un nodo di uno
Heap di Fibonacci
composto da
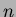
nodi é
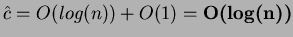
.
Dimostrazione:
Sia 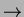 un nodo di heap di Fibonacci composto da
un nodo di heap di Fibonacci composto da 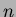 nodi e sia
nodi e sia
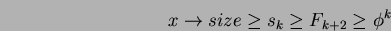 . Possiamo dire che
. Possiamo dire che
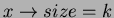 dato il
Lemma 3. Utilizzando
dato il
Lemma 3. Utilizzando 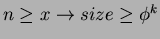 si ottiene
si ottiene
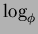 , cioè
, cioè
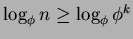 .
Il grado massimo (quello che noi avevamo chiamato
.
Il grado massimo (quello che noi avevamo chiamato 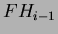 ) di un qualunque
nodo di uno heap di Fibonacci è dunque
) di un qualunque
nodo di uno heap di Fibonacci è dunque
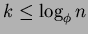




Next: L'utilizzo degli Heap di
Up: Gli Heap di Fibonacci
Previous: Operazioni - Cancellazione di
Indice
Paolo Larcheri
2002-01-26
![]() size il numero di nodi dell'albero
radicato in x (compreso x stesso). La dimostrazione mostra
anche come x
size il numero di nodi dell'albero
radicato in x (compreso x stesso). La dimostrazione mostra
anche come x![]() size è esponenziale a
x
size è esponenziale a
x![]() grado.
grado.
![]() -esimo numero di Fibonacci è:
-esimo numero di Fibonacci è:
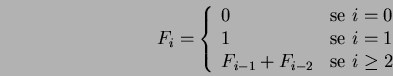 può essere espresso in un'altro modo:
può essere espresso in un'altro modo:

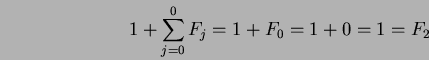 ,
si ha:
,
si ha:
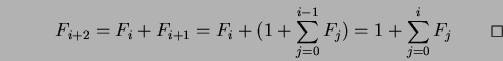 il cosiddetto rapporto aureo definito come
il cosiddetto rapporto aureo definito come
 e
e 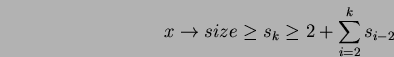 .
I casi di base (per
.
I casi di base (per 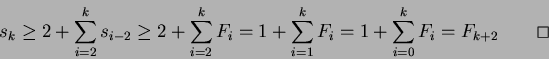
![]() un nodo di heap di Fibonacci composto da
un nodo di heap di Fibonacci composto da ![]() nodi e sia
nodi e sia
![]() . Possiamo dire che
. Possiamo dire che
![]() dato il
Lemma 3. Utilizzando
dato il
Lemma 3. Utilizzando ![]() si ottiene
si ottiene
![]() , cioè
, cioè
![]() .
Il grado massimo (quello che noi avevamo chiamato
.
Il grado massimo (quello che noi avevamo chiamato ![]() ) di un qualunque
nodo di uno heap di Fibonacci è dunque
) di un qualunque
nodo di uno heap di Fibonacci è dunque
![]()