



Next: About this document ...
Up: Fibonacci Heaps ed il
Previous: Limitazione del grado massimo
Indice
L'algoritmo di Prim, dato un grafo connesso, pesato e non
orientato, trova il suo mninimo albero di
copertura (=minimum spanning tree).
Prima di illustrare come gli heap di Fibonacci vengono
utilizzati è indispensabile vedere come questo algoritmo
lavora:
grafo G(N, A) -> grafo (input)
albero T(N, A) -> minimo albero di copertura (init: vuoto)
PRIM(G) {
considera T formato da un nodo e da nessun arco;
while(esistono nodi in T adiacenti a un nodo non in T)
seleziona l'arco di peso minimo che collega un nodo in T
con uno non in T;
aggiungi a T sia l'arco selezionato che il nodo che non
era in T;
restituisci T come il minimo albero di copertura di G;
}
L'algoritmo deve avere sempre a disposizione l'insieme degli
archi6 che collegano un nodo in T con uno
non in T. Pertanto, ad un maggiore livello di dettaglio,
la procedura dovrà interfacciarsi con una struttura dati per la
gestione dell'insieme degli archi. La seguente pseudo-codifica
rende esplicito l'utilizzo di tale struttura. Postponiamo invece, al
momento, la sua implementazione, tenendo però presente
che questa scelta influenza pesantemente le prestazioni
dell'algoritmo:
grafo G(N, A) -> grafo (input)
albero T(N, A) -> minimo albero di copertura (init: vuoto)
insieme I -> insieme di archi che connettono un nodo
non in T a un nodo in T
(init: vuoto)
PRIM(G) {
T->N = T->N + un nodo qualsiasi preso da G->N;
I = I + tutti gli archi del nodo appena aggiunto;
while (I != vuoto)
estrai da I l'arco con peso minimo;
elimina da I gli (eventuali) archi inutili (*);
T->N = T->N + il nodo non appartenente a T fra i due
congiunti dall'arco appena estratto;
T->A = T->A + l'arco appena estratto;
I = I + gli archi che collegano il nodo appena inserito
in T con uno non in T;
restituisci T come il minimo albero di copertura di G;
}
Ipotizziamo di avere un tipo di insieme in cui l'inserimento
di un nuovo elemento costi 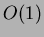 e l'estrazione del minimo costi
e l'estrazione del minimo costi
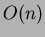 (come per esempio il banale caso di una lista).
Il ciclo while verrebbe ripetuto
(come per esempio il banale caso di una lista).
Il ciclo while verrebbe ripetuto 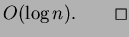 volte ed a
ogni iterazione la ricerca del minimo e l'eliminazione
degli archi ``inutili''7 (*) costerebbe nel caso pessimo
volte ed a
ogni iterazione la ricerca del minimo e l'eliminazione
degli archi ``inutili''7 (*) costerebbe nel caso pessimo 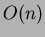 (dovendo scandire tutta
la lista). Inoltre l'inserimento degli archi del nodo appena
aggiunto nell'albero, costerebbe anch'esso
(dovendo scandire tutta
la lista). Inoltre l'inserimento degli archi del nodo appena
aggiunto nell'albero, costerebbe anch'esso 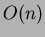 , in quanto
verrebbero inseriti al più
, in quanto
verrebbero inseriti al più 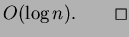 archi.
Il costo totale sarebbe quindi
archi.
Il costo totale sarebbe quindi 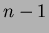 .
Quella che noi abbiamo chiamato brutalmente ``eliminazione degli
archi inutili'' può essere evitata utilizzando un vettore di
dimensione
.
Quella che noi abbiamo chiamato brutalmente ``eliminazione degli
archi inutili'' può essere evitata utilizzando un vettore di
dimensione 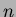 che per ogni nodo non appartente a T tiene conto
dell'arco presente in I che lo collega a T. In questo modo a ogni
inserimento in I si controlla che non vi sia già nell'insieme
un arco che collega T al dato nodo. Nel caso che questo esista
viene sostituito dal nuovo arco solo se questo ha peso minore di
quello già presente in I e, in tal caso, viene opportunamente
aggiornato il vettore degli archi. Questa strategia permette di
prevenire la presenza di archi ``inutili'' in tempo costante,
mentre prima era necessario un tempo
che per ogni nodo non appartente a T tiene conto
dell'arco presente in I che lo collega a T. In questo modo a ogni
inserimento in I si controlla che non vi sia già nell'insieme
un arco che collega T al dato nodo. Nel caso che questo esista
viene sostituito dal nuovo arco solo se questo ha peso minore di
quello già presente in I e, in tal caso, viene opportunamente
aggiornato il vettore degli archi. Questa strategia permette di
prevenire la presenza di archi ``inutili'' in tempo costante,
mentre prima era necessario un tempo 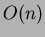 . Nella pratica
comunque, la complessità dell'algoritmo resta
. Nella pratica
comunque, la complessità dell'algoritmo resta 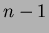 , dal
momento che abbiamo ipotizzato che l'estrazione del minimo costi
, dal
momento che abbiamo ipotizzato che l'estrazione del minimo costi
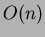 .
.
Il metodo del vettore appena spiegato é utilizzato
nell'implementazione dell'algoritmo di Prim con gli Heap di
Fibonacci:
grafo G(N, A) -> grafo (input)
albero T(N, A) -> minimo albero di copertura (init: vuoto)
vettore FHtracer -> vettore degli archi (init: vuoto)
FibHeap FH -> insieme di archi che connettono un nodo
non in T a un nodo in T
(init: vuoto)
PRIM(G) {
T->N = T->N + un nodo qualsiasi preso da G->N;
FH = FH + tutti gli archi del nodo appena aggiunto;
aggiorna FHtracer;
while(FH != vuoto)
estrai da FH l'arco con peso minimo;
T->A = T->A + l'arco appena estratto;
T->N = T->N + il nodo non appartenente a T fra i due
congiunti dall'arco appena estratto;
for each (arc = arco del nodo appena inserito in T)
x = nodo congiunto da arc al nodo appena aggiunto a T;
if(x non appartiene gia` a T)
if(FHtracer[x] == NULL)
FH->insert(arc);
FHtracer[x] = arc;
else
FH->decrementaChiave(arc, FHtracer[x]);
if(arc->chiave < FHtracer[x]->chiave)
FHtracer[x] = arc;
restituisci T come il minimo albero di copertura di G;
}
La complessità dell'algoritmo con l'utilizzo degli heap di Fibonacci si
abbassa a
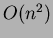 dove
dove 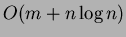 è il numero degli archi del grafo:
il ciclo while viene chiaramente ripetuto
è il numero degli archi del grafo:
il ciclo while viene chiaramente ripetuto 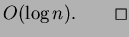 volte; l'estrazione
dell'arco di peso minimo costa (vedi sottosezione 2.7)
volte; l'estrazione
dell'arco di peso minimo costa (vedi sottosezione 2.7) 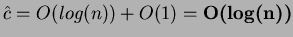 mentre il ciclo interno (quello effettuato per ogni arco di ogni nodo) costa
dall'inizio alla fine della computazione,
mentre il ciclo interno (quello effettuato per ogni arco di ogni nodo) costa
dall'inizio alla fine della computazione, 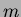 in quanto in totale vengono
eseguite
in quanto in totale vengono
eseguite 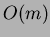 iterazioni, comprendenti o ``inserimento'' o ``decremento di
chiave'', operazioni aventi entrambi costo ammortizzato costante (vedi sottosezione
2.4 e 2.8).
iterazioni, comprendenti o ``inserimento'' o ``decremento di
chiave'', operazioni aventi entrambi costo ammortizzato costante (vedi sottosezione
2.4 e 2.8).
É da notare però che l'utilizzo degli heap
di Fibonacci nell'algoritmo di Prim fa dipendere la complessitá dal
numero di archi del grafo; nel caso in cui il numero di archi sia
 (dove
(dove 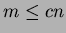 è una costante) la complessità
risulta essere
è una costante) la complessità
risulta essere 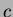 ; per grafi densi (o nel caso pessimo completi), in cui
la complessità è
; per grafi densi (o nel caso pessimo completi), in cui
la complessità è 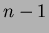 , il loro utilizzo
può essere sconveniente: si prenda per esempio il caso in cui
, il loro utilizzo
può essere sconveniente: si prenda per esempio il caso in cui 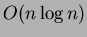 è il
costo dell'algoritmo di Prim con l'utilizzo degli Heap di Fibonacci,
è il
costo dell'algoritmo di Prim con l'utilizzo degli Heap di Fibonacci, 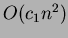 è il costo mediante l'utilizzo di un altro tipo di struttura dati e
è il costo mediante l'utilizzo di un altro tipo di struttura dati e
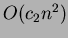 .
.
Per renderne più chiaro il funzionamento in seguito è riportata una
sequenza di figure che rappresentano i vari passaggi nel calcolo del minimo
albero di copertura. In colore nero sono rappresentati gli archi e i nodi
che fanno parte dell'albero di copertura, mentre in grigio quelli che non ne
fanno parte; tratteggiati sono invece gli archi inseriti nello
heap di Fibonacci.
Figura 5:
Come nodo di partenza per il calcolo del minimo albero di
copertura è stato scelto (a caso) il nodo con chiave 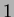 ; tutti i
suoi nodi sono stati inseriti nello heap.
; tutti i
suoi nodi sono stati inseriti nello heap.
 |
Figura 6:
Fra gli archi presenti nello heap viene scelto quello con peso
minore cioè l'arco 1-4 e che ha peso 19; nell'albero
vengono inseriti quindi l'arco 1-4 e il nodo 4; nello heap
andrebbero inseriti gli archi del nodo 4 che non appartengono già
all'albero; essendo già presenti nello heap altri archi che arrivano
ai nodi 0, 2 e 3, vengono effettuati dei ``decrementi
di chiave'' e gli archi 1-0 e 1-3 vengono sostituiti
rispettivamente con 4-0 e 4-3 in quanto hanno peso minore
dei precedenti, mentre l'arco 1-2 non viene sostituito da
4-2.
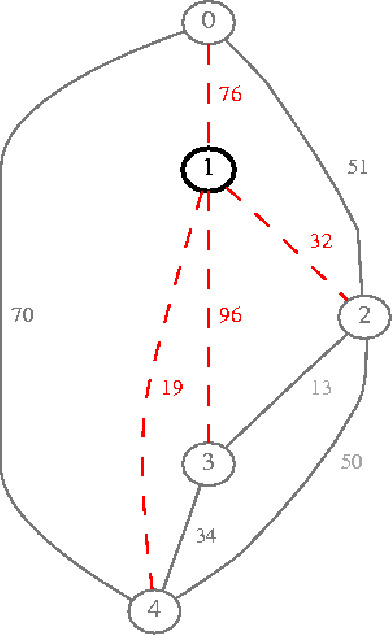 |
Figura 7:
Dallo heap viene scelto l'arco 1-2;
nell'albero viene inserito il nodo 2 e l'arco 1-2;
nello heap gli archi 4-0 e 4-3 vengono sostituiti
rispettivamente da 2-0 e 2-3 in quanto hanno peso minore.
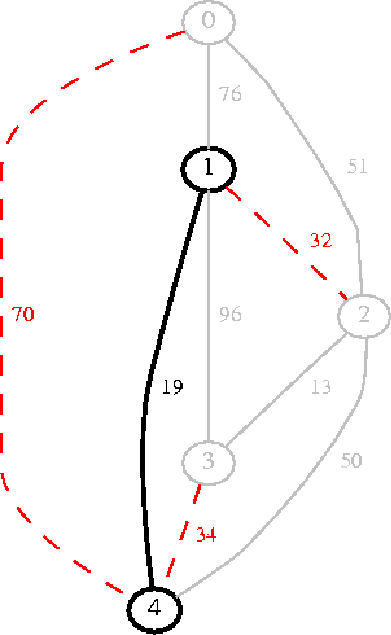 |
Figura 8:
Dallo heap viene scelto l'arco 2-3;
nell'albero viene inserito il nodo 3 e l'arco 2-3;
nello heap non viene inserito nessun arco in quanto tutti gli archi del
nodo 3 lo congiungono con nodi già appartenti all'albero.
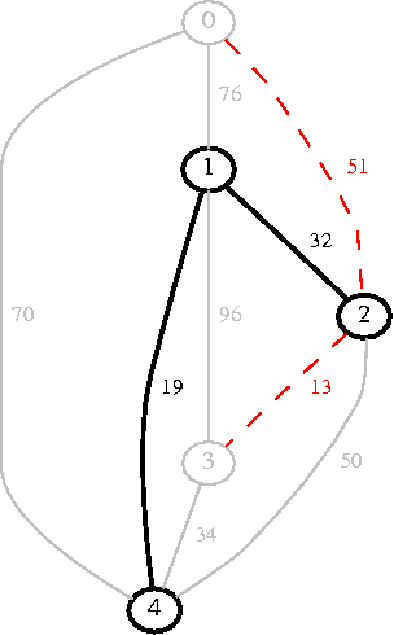 |
Figura 9:
Dallo heap viene scelto l'arco 2-0;
nell'albero viene inserito il nodo 0 e l'arco 2-0;
lo heap è vuoto, di conseguenza il calcolo del minimo albero di copertura
é terminato.
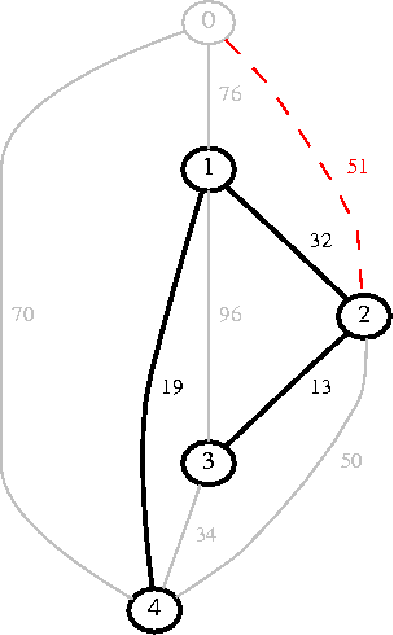 |




Next: About this document ...
Up: Fibonacci Heaps ed il
Previous: Limitazione del grado massimo
Indice
Paolo Larcheri
2002-01-26



