pnd: puntatore al nodo la cui chiave va decrementata
nk: nuovo valore della chiave
ppd: puntatore al padre
DECREMENTA-CHIAVE(pnd, nk) {
if (nk > pnd->chiave)
Errore;
pnd->chiave = nk;
ppd = pnd->ppadre;
if(ppd != NULL) e (pnd->chiave < ppd->chiave)
TAGLIA(pnd, ppd);
TAGLIO-A-CASCATA(ppd);
if(pnd->chiave < FH->min->chiave)
FH->min = pnd;
}
Il primo passo consiste nel confrontare il nuovo valore della chiave con
quello vecchio: se il vecchio è minore del nuovo è chiaramente
restituito errore; in caso contrario il campo chiave del nodo assume
il nuovo valore; in seguito si controlla se il padre del nodo in questione
ha chiave maggiore del figlio: in caso positivo va ristabilita la
proprità degli Heap secondo cui un nodo ha sempre chiave maggiore
o uguale al padre (se questo esiste).
Per compiere questo vengono chiamate le funzioni ausiliarie TAGLIA e
TAGLIO-A-CASCATA. Come ultima cosa viene, se necessario, aggiornato il
puntatore al minimo.
Funzionamento della funzione TAGLIO:
TAGLIO(pnd, ppd) {
toglie pnd dalla lista dei figli di ppd;
ppd->grado = ppd->grado -1;
pnd->ppadre = NULL;
pnd->marcato = false;
}
Funzionamento della funzione TAGLIO-A-CASCATA:
TAGLIO-A-CASCATA(pnd) {
ppd = pnd->ppadre;
if(ppd!=NULL)
if(pnd->marcato == false)
pnd->marcato = true;
else
TAGLIO(pnd, ppd);
TAGLIO-A-CASCATA(ppd);
}
Per capire meglio il procedimento di decremento della chiave di un nodo e
tutto quello che ne consegue è utile chiarirsi le idee con un esempio:
in Fig.4 sono raffigurati i vari stati dello Heap durante il decremento di due chiavi ed i successivi tagli:
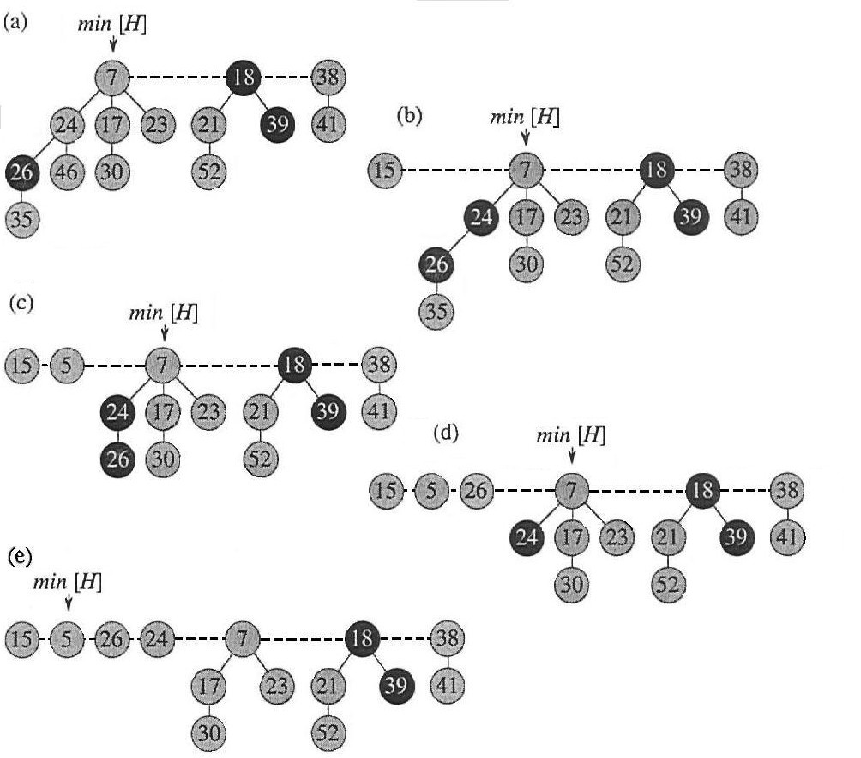 prende chiave
prende chiave
A cosa serve fare tutti questi tagli se concretamente sarebbe stato
sufficiente fare solo il taglio del nodo la cui radice è stata
decrementata?
La risposta è semplicissima: il procedimento permette alla
DECREMENTA-CHIAVE di avere costo ammortizzato pari a ![]() :
supponiamo che la TAGLIO-A-CASCATA sia richiamata
:
supponiamo che la TAGLIO-A-CASCATA sia richiamata ![]() volte dopo la chiamata
a DECREMENTA-CHIAVE; il costo della DECREMENTA-CHIAVE stessa è
volte dopo la chiamata
a DECREMENTA-CHIAVE; il costo della DECREMENTA-CHIAVE stessa è ![]() e
cosí anche per la singola chiamata a TAGLIO-A-CASCATA (senza le chiamate
ricorsive): quindi il costo reale della
e
cosí anche per la singola chiamata a TAGLIO-A-CASCATA (senza le chiamate
ricorsive): quindi il costo reale della
DECREMENTA-CHIAVE è
![]() .
.
Il cambio di potenziale dello Heap:
Ora risulta anche chiaro il motivo per cui la funzione potenziale degli Heap di Fibonacci sia stata definita con il doppio del numero di nodi marcati: in questo modo il costo ammortizzato della DECREMENTA-CHIAVE risulta essere costante.