



Next: Operazioni - Decremento di
Up: Gli Heap di Fibonacci
Previous: Operazioni - Unione di
Indice
L'operazione di estrazione del nodo minimo costituisce, per quel che riguarda
gli Heap di Fibonacci, il lavoro più complesso in quanto prevede la
ristrutturazione dello Heap, che nelle altre funzioni non é presente.
Infatti la funzione di estrazione del minimo (come si puo' vedere dallo
``pseudo-codice'') utilizza due funzioni ausiliarie il cui funzionamento è
spiegato in seguito:
ESTRAI-MIN() {
minimo = FH->min;
if(FH->min != NULL)
for(ogni figlio x di FH->min)
togli x dala lista dei figli di min;
aggiungi x alla lista delle radici di FH;
x->ppadre = NULL;
FH->nalberi = FH->nalberi + 1;
if(FH->nnodi == 1)
FH->min = NULL;
FH->nalberi = FH->nalberi - 1;
else
FH->min = FH->min->pdestro;
CONSOLIDATE(); <- funzione di ristrutturazione dello Heap
FH->nnodi = FH->nnodi - 1;
return minimo;
}
La ESTRAI-MIN() accede direttamente al minimo grazie al campo min dello Heap,
``promuove'' ogni suo figlio a radice; se il minimo era l'unico nodo mette il campo
min a NULL, altrimenti gli assegna il suo adiacente destro (che non
necessariamente è realmente il nuovo minimo) ed esegue la funzione di
restaurazione; infine viene appropriatamente aggiornato il campo contatore dei
numeri di nodi dello Heap e viene ritornato il nodo con chiave minima.
Chiaramente se lo Heap è vuoto viene ritornato NULL.
La CONSOLIDATE() ha il compito di ricompattere il più possibile gli alberi; tale
operazione eseguirà ripetutamente i seguenti due passi:
- -
- trovare due radici con lo stesso grado;
- -
- ``trasformare'' quella con chiave più piccola in un figlio di quella con
chiave maggiore.
Il secondo dei due passi è effettuato dalla LINK, un'altra funzione ausiliaria il
cui (semplice) funzionamento è spiegato in seguito. Vediamo una possibile
implementazione della CONSOLIDATE:
R[ ]: vettore di puntatori alle radici (init: NULL),
R[i] punta all'ultima radice di grado i incontrata
x, y: puntatori alle radici correnti
g: contiene il grado dell'ultima radice considerata
CONSOLIDATE() {
R[i] = NULL per ogni i;
for(ogni nodo nd della lista della radici di FH)
g = nd->grado;
x = nd;
while(R[g] != NULL)
y = R[g];
if(x->chiave > y->chiave)
swap(x, y);
LINK(y, x);
R[g] = NULL;
g = g+1;
R[g] = x;
FH->min = NULL;
for(ogni i fino alla fine di R[ ])
if (R[i] != NULL)
aggiungi R[i] alla lista delle radici;
if(FH->min == NULL)oppure(R[i]->chiave < FH->min->chiave)
FH->min = R[i];
}
Per ogni radice dello Heap controlla se è stata precedentemente incontrata
un'altra radice con lo stesso grado: in caso affermativo quella con chiave minore
viene ``linkata'' all'altra (con la chiamata della funzione LINK), il grado
della radice-padre viene incrementato e viene effettuato nuovamente lo stesso
controllo. In caso negativo invece, la radice viene memorizzata nel vettore ![$R[]$](img71.png) alla posizione
alla posizione 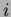 , dove
, dove 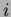 è il grado della radice stessa.
è il grado della radice stessa.
Infine viene aggiornato il campo min e ricreata la lista delle radici:
viene scandito tutto il vettore ![$R[]$](img71.png) inserendo una ad una ogni radice presente in
esso.
inserendo una ad una ogni radice presente in
esso.
La funzione LINK serve per fondere due alberi in uno; la radice di uno dei due
(quella con chiave minore) diventa un nodo figlio della radice dell'altro:
LINK(y, x) {
togli y dalla lista delle radici di FH;
aggiungi y alla lista dei figli di x;
x->grado = x->grado + 1;
y->marcato = false;
}
Figura 3:
(a): lo heap prima dell'estrazione;
(b): viene estratto il minimo e tutti i suoi figli sono promossi a
radice;
(c): inizia la scansione della lista delle radici:  ha grado
1;
(d):
ha grado
1;
(d):  ha grado
ha grado 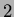 ;
(e):
;
(e): 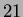 ha grado
ha grado 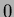 ;
(f):
;
(f): 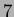 ha grado
ha grado 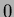
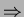
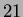 linkato a
linkato a 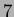 ;
(g): ora
;
(g): ora 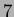 ha grado 1
ha grado 1 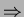
 linkato a
linkato a 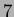 ;
(h): ora
;
(h): ora 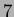 ha grado 2
ha grado 2 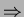
 linkato a
linkato a 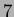 ;
(i):
;
(i): 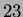 ha grado
ha grado 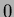 ;
(j):
;
(j): 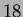 ha grado
ha grado 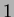 ;
(k):
;
(k): 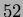 ha grado
ha grado 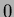
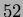 linkato a
linkato a 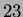 ;
ora
;
ora 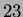 ha grado
ha grado 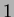
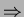
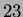 linkato a
linkato a 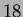 ;
` (l):
;
` (l): 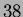 ha grado
ha grado 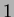 ;
(m): lo heap é finalmente restaurato!
;
(m): lo heap é finalmente restaurato!
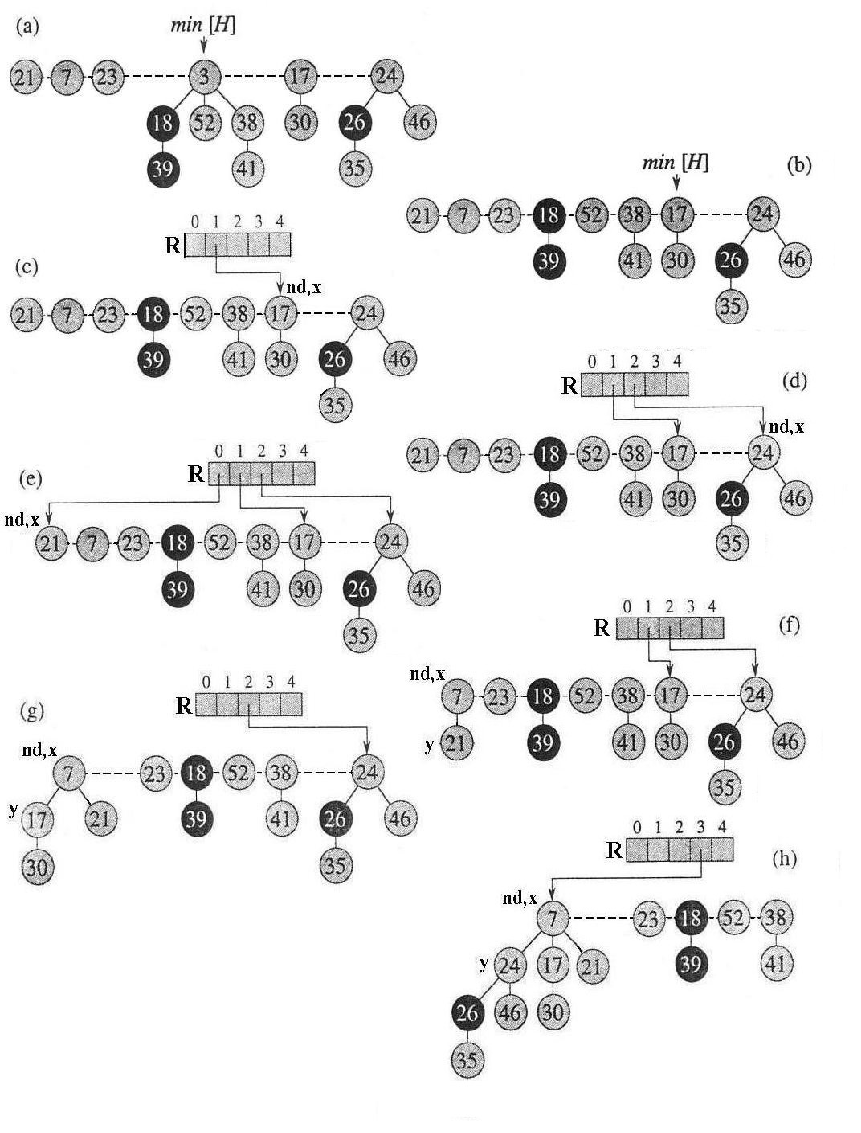 |
In Fig. 3 è mostrato il processo di estrazione del
minimo(ESTRAI-MIN) e di restaurazione dello Heap (CONSOLIDATE e LINK).
Per il calcolo del costo della ESTRAI-MIN è indispensabile assumere che esiste un
limite superiore 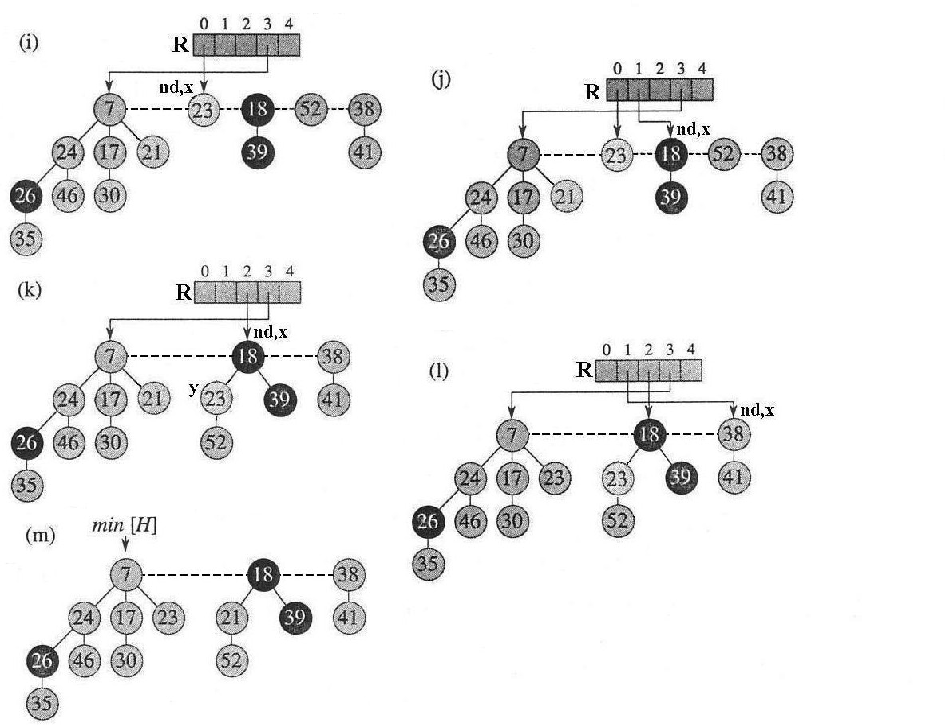 al grado massimo di un nodo qualsiasi dello Heap di
Fibonacci; questo fatto verrà dimostrato in seguito (sottosezione 2.10).
Affinchè il costo della ESTRAI-MIN sia ottimale è ovvio che la dimensione di
al grado massimo di un nodo qualsiasi dello Heap di
Fibonacci; questo fatto verrà dimostrato in seguito (sottosezione 2.10).
Affinchè il costo della ESTRAI-MIN sia ottimale è ovvio che la dimensione di
![$R[]$](img71.png) debba essere anch'essa ottimale in quanto tale vettore viene più
volte scandito e questo fatto potrebbe fare aumentare il costo totale; la sua
dimensione sará
debba essere anch'essa ottimale in quanto tale vettore viene più
volte scandito e questo fatto potrebbe fare aumentare il costo totale; la sua
dimensione sará 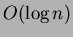 che è proprio il grado massimo che una radice
può avere.
che è proprio il grado massimo che una radice
può avere.
Dimostriamo ora che il costo ammortizzato della ESTRAI-MIN è 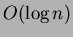 : un
contributo pari a
: un
contributo pari a 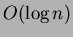 è dato dal ciclo che promuove a radice tutti gli
è dato dal ciclo che promuove a radice tutti gli
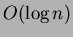 figli del nodo minimo; vi sono poi l'inizializzazione del vettore
figli del nodo minimo; vi sono poi l'inizializzazione del vettore
![$R[]$](img71.png) (all'inizio della CONSILIDATE) e la ricreazione della lista delle radici dello
Heap (alla fine della CONSOLIDATE) che consitono entrambe nello scandire
(all'inizio della CONSILIDATE) e la ricreazione della lista delle radici dello
Heap (alla fine della CONSOLIDATE) che consitono entrambe nello scandire ![$R[]$](img71.png) e che
quindi portano un contributo pari anch'esso a
e che
quindi portano un contributo pari anch'esso a 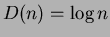 .
.
Resta ora da considerare la parte centrale della funzione CONSOLIDATE, quella
incaricata di trovare e fondere gli alberi di uguale dimensione; il ciclo in
questione opera una scansione della lista delle radici: tale lista è al più
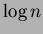 dal momento che è formata dalla vecchia lista delle radici (
dal momento che è formata dalla vecchia lista delle radici (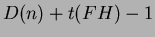 )
e dai figli del nodo con chiave minima (D(n)); inoltre ad essa è stato tolto il
minimo (-1). Quindi il costo reale totale in questo caso è
)
e dai figli del nodo con chiave minima (D(n)); inoltre ad essa è stato tolto il
minimo (-1). Quindi il costo reale totale in questo caso è
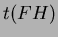 .
Trovato il costo reale non resta che il calcolo del potenziale per avere al termine
il costo ammortizzato.
Il potenziale prima:
.
Trovato il costo reale non resta che il calcolo del potenziale per avere al termine
il costo ammortizzato.
Il potenziale prima:
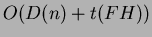
e dopo:
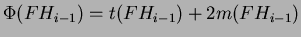
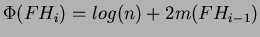
Notiamo subito che il potenziale di 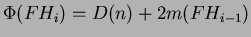 è minore o uguale a quello di
è minore o uguale a quello di
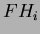 in quanto il numero di radici dopo la ristrutturazione dello Heap è
diventato al più
in quanto il numero di radici dopo la ristrutturazione dello Heap è
diventato al più 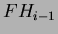 (esattamente come il numero di radici in uno
Heap Binomiale).
(esattamente come il numero di radici in uno
Heap Binomiale).
Il costo ammortizzato come al solito è:
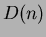
sostituendo i due potenziali:
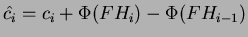
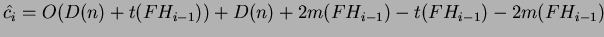
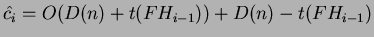
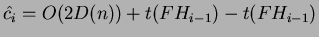
dal momento che 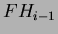 è stato assunto come
è stato assunto come 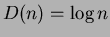 , si ha:
, si ha:
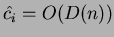




Next: Operazioni - Decremento di
Up: Gli Heap di Fibonacci
Previous: Operazioni - Unione di
Indice
Paolo Larcheri
2002-01-26

 al grado massimo di un nodo qualsiasi dello Heap di
Fibonacci; questo fatto verrà dimostrato in seguito (sottosezione 2.10).
Affinchè il costo della ESTRAI-MIN sia ottimale è ovvio che la dimensione di
al grado massimo di un nodo qualsiasi dello Heap di
Fibonacci; questo fatto verrà dimostrato in seguito (sottosezione 2.10).
Affinchè il costo della ESTRAI-MIN sia ottimale è ovvio che la dimensione di