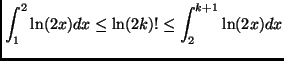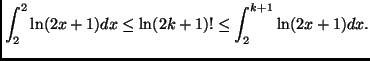Next: Esercizio 3
Up: doneScrittoII
Previous: Esercizio 1
Il semifattoriale di un intero positivo 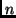 è il prodotto di tutti
gli interi positivi non maggiori di
è il prodotto di tutti
gli interi positivi non maggiori di 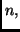 aventi la stessa parità di
aventi la stessa parità di 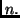
Ad esempio,
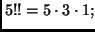
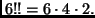
Trovare una semplice 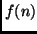 per cui si abbia
per cui si abbia
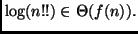 Dimostrare il risultato trovato, senza
dare per buoni i fatti visti a lezione riguardo a
Dimostrare il risultato trovato, senza
dare per buoni i fatti visti a lezione riguardo a 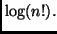
Si può ricostruire, per esempio attraverso il disegno con l'integrale, il
risultato visto a lezione, trovando quindi che
A questo, punto, distinguiamo due casi a seconda della parità di n.
- se
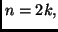 allora
da cui,
o piú semplicemente
da cui, tornando a
allora
da cui,
o piú semplicemente
da cui, tornando a 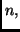
- se
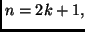 allora possiamo sfruttare il fatto che
allora possiamo sfruttare il fatto che
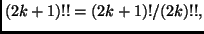 ed usare il punto precedente. Piú
sbrigativo è ricorrere al punto precedente notando semplicemente che
ed usare il punto precedente. Piú
sbrigativo è ricorrere al punto precedente notando semplicemente che
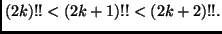
L'esercizio si poteva anche risolvere piú direttamente notando che
e che
Romeo Rizzi
2003-03-07