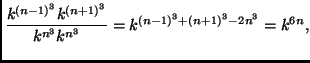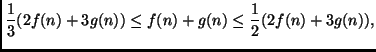
L'uguaglianza sussiste invece con l'ipotesi aggiuntiva
![]()
Qualche tentativo: prima con una funzione polinomiale, e.g.
![]() Abbiamo
Abbiamo
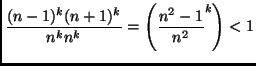
Indi con una funzione esponenziale: ![]()
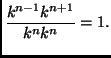
Anche con
![]()
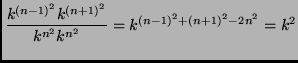
Con
![]() tuttavia, le cose cambiano:
ad es. con
tuttavia, le cose cambiano:
ad es. con
![]() si ha
si ha