Esercizio 3

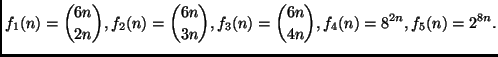
Mettere le seguenti funzioni in ordine di crescita non decrescente, segnalando le funzioni che avessero eventualmente lo stesso ordine di crescita:

$$f_1(n)= {{6n} \choose {2n}}, f_2(n)= {{6n} \choose {3n}}, f_3(n)= {{6n} \choose {4n}}, f_4(n)= 8^{2n}, f_5(n)= 2^{8n}.$$

È concesso usare, se necessario, la formula di Stirling.

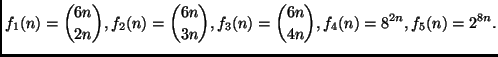
Per le proprietà di simmetria dei coefficienti binomiali, intanto, notiamo che $f_1(n)= f_3(n).$ Siccome poi i coefficienti binomiali crescono verso il centro, $f_2(n)$ è maggiore di entrambe le precedenti funzioni; ricordiamo che esso è il massimo tra i coefficienti della riga $6n$ del triangolo di Tartaglia.

Ricordiamo poi che i coefficienti di detta riga sommano a $2^{6n},$ che è precisamente $f_4(n),$ la quale cresce ovviamente meno di $f_5(n)$. Con considerazioni istantanee siamo dunque arrivati a dire che

$$f_1(n)= f_3(n) \leq f_2(n) \leq f_4(n) < f_5(n).$$

Servono due ulteriori indagini riguardo ai segni $\leq$ per stabilire se essi siano dei minori stretti o delle uguaglianze. Notiamo che

$$\frac{f_1(n)}{f_2(n)} = \frac{\frac{6n !}{2n ! 4n !}}{\frac{6n!}{3n! 3n!}}$$

$$= \frac{3n ! 3n !}{2n ! 4n!}$$

$$= \frac{(3n)(3n-1) \ldots (2n+1)}{(4n)(4n-1) \ldots (3n+1)}$$

$$= \frac{3n}{4n} \, \frac{3n-1}{4n-1} \, \ldots \frac{2n+1}{3n+1}$$

$$= \leq \left( \frac{3}{4} \right)^n$$

rapporto che tende a zero; gli ordini di grandezza sono dunque diversi.

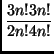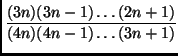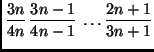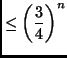L'altro dubbio si può risolvere usando la formula di Stirling, come da suggerimento. Abbiamo

$${{6n} \choose {3n}} = \frac{6n !}{{(3n !)}^2} = \frac{\sqrt{2 \pi 6 n} \left( \frac{6n}{e} \right)^{6n}}{2 \pi 3 n \left( \frac{3n}{e} \right)^{6n}} (1 + \Theta(1/n))$$

$$= \sqrt{\frac{1}{3 \pi n}} 2^{6n} (1 + \Theta(1/n))$$

da cui si vede che anche questo minore è stretto.

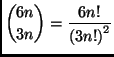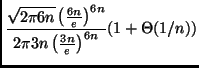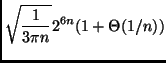N.B.: il teorema limite centrale del calcolo delle probabilità è un'alternativa alla formula di Stirling per dimostrare in maniera molto rapida che $\lim_{n \rightarrow \infty} f_2(n) / f_4(n) = 0.$