Svolgimento della Provetta sulla Programmazione Combinatoria


ESERCIZIO 1:


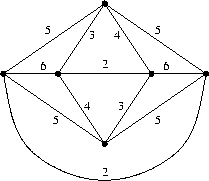
\begin{figure}% \begin{center} \leavevmode \psfig{figure=tree.eps, height=4 true cm}\par\end{center}\end{figure}

1.
Trovare l'albero ricoprente di peso minimo.
2.
Fornire un'argomentazione per l'ottimalità.
3.
Indicare quali archi siano contenuti in ogni soluzione ottimale.
4.
Indicare quali archi non siano contenuti in alcuna soluzione ottimale.
5.
Sfruttare le informazioni di cui ai punti 3. e 4. per rappresentare in modo compatto l'insieme delle soluzioni ottime o quantomeno fornire tutte le soluzioni ottime.

L'algoritmo di Prim parte da un nodo e cresce un'arborescenza aggiungendo un nodo alla volta: quello reggiungibile attraverso un arco di minor costo. Quando l'alborescenza ricopre tutti i nodi essa é un albero ricoprente di peso minimo.

\psfig{figure=prim.eps, height=7.8 true cm}

PROVA DI OTTIMALITÀ: Sia T l'albero ricoprente di cui voglio dimostrare l'ottimalità. Per ogni arco $e\in T$ fornisco un taglio $\delta(S_e)$ tale che

\begin{displaymath}T\cap \delta(S_e)=\{e\} \mbox{ \ ed inoltre \ } c(e)= \min_{f\in \delta(S_e)} c(f) \end{displaymath}


\begin{figure}% \begin{center} \leavevmode \psfig{figure=cutProve.eps, height=4.5 true cm}\par\end{center}\end{figure}

Esercizio 1   Perchè un tale insieme di tagli, se presente, costituisce prova di ottimalità?

Esercizio 2   Dimostrare che esiste sempre una tale prova di ottimalità.

Suggerimento: dimostrare prima che ogni albero ha almeno una foglia (di fatto almeno due), dove per foglia si intende un nodo di grado 1.

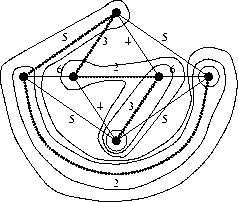
Consideriamo ora una seconda via per certificare l'ottimalità di un albero ricoprente T: si dà una familia $\cal S$ di n-1 sottoinsiemi propri $S_1, S_2, \ldots, S_{n-1}$di V(G) dove ciascun Si è ottenuto da Si-1tramite l'aggiunta di un singolo nodo si. In particolare S1 contiene precisamente un nodo s1. Gli archi in T sono pure n-1. Si richiede che ad ogni arco $e\in T$ sia associato un taglio Se di $\cal S$ con $e\in S_e$ e tale che

\begin{displaymath}c(e)= \min_{f\in \delta(S_e)} c(f) \end{displaymath}

con la condizione che ad archi diversi siano associati tagli diversi. Ad esempio:


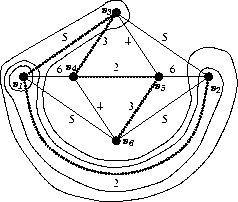
\begin{figure}% \begin{center} \leavevmode \psfig{figure=primProve.eps, height=4.5 true cm}\par\end{center}\end{figure}

Esercizio 3   Indicare in figura anche i tagli S4,S5 ed S6. (Consiglio di utilizzare diversi colori). Indicare inoltre quali archi di T sono associati ai vari tagli. (Avvalersi ancora dei colori).

Esercizio 4   Perchè un tale insieme di tagli, se presente, costituisce prova di ottimalità?

Osserviamo come la famiglia dei tagli proposti era di fatto ricavata dall'algoritmo di Prim.

Domanda 5   Posso sempre fornire una tale prova di ottimalità? Perchè?

Esercizio 6   Ma allora nell'Esercizio 4 abbiamo di fatto dimostrato la correttezza dell'algoritmo Prim. Vero?

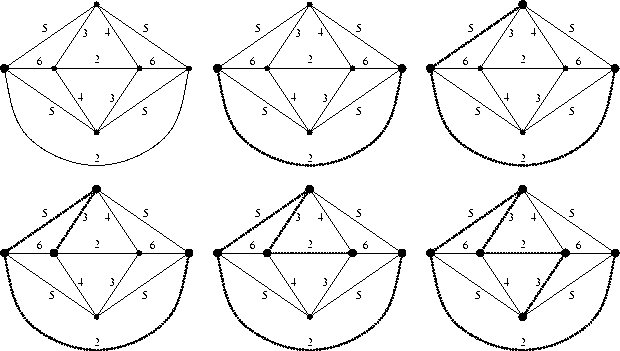
L'algoritmo di Kruskal ordina dapprima gli archi per peso non decrescente. Gli archi vengono quindi esaminati uno alla volta seguendo tale ordine ed inclusi nella soluzione se e solo se la loro introduzione non porta alla formazione di circuiti.


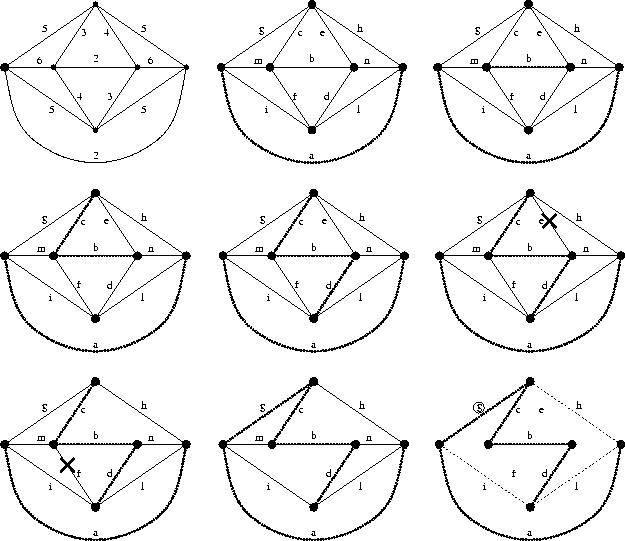
\begin{figure}% \begin{center} \leavevmode \psfig{figure=krusk.eps, height=12 true cm}\par\end{center}\end{figure}

Nel proseguio dell'algoritmo abbiamo deciso di rimuovere dal grafo quegli archi e la cui aggiunta porterebbe a dei circuiti Ce con ce > cfper ogni $f\in C_e$. Se invece Ce contiene un arco fcon c(f)=c(e) (il caso c(f)>c(e)non può mai verificarsi visto che gli archi sono stati ordinati per peso non decrescente) allora l'arco e non viene incluso nella soluzione ottima ma resta tratteggiato; l'arco f viene inoltre detto sostituibile (perchè?). Ciò porta all'ultimo grafo in figura. Gli archi rimossi non possono appartenere ad alcuna soluzione ottima. Per ciascun arco tratteggiato esiste una soluzione ottima che lo contiene; tale soluzione verrà prodotta da Kruskal partendo da un differente ordinamento non decrescente. Le quattro soluzioni ottime sono quindi evidenti nell'ultimo grafo in figura. L'unico arco che risulta sostituibile è l'arco g. Gli archi a,b,c e d sono pertanto inclusi in ogni soluzione ottima.

PROVA DI OTTIMALITÀ: Sia T l'albero ricoprente di cui voglio dimostrare l'ottimalità. Per ogni arco $e\notin T$fornisco un circuito Ce tale che

\begin{displaymath}c(e) \geq \max_{f\in C_e} c(f) \end{displaymath}

Ovviamente posso restingermi a cercare tale circuito in $T\cup \{e\}$. E tuttavia sappiamo che $T\cup \{e\}$contiene un unico circuito, detto circuito fondamentale di e in T. Esso è pertanto il circuito Ce desiderato. Osserviamo come l'algoritmo di Kruskal, ogni volta che esclude un arco e, già ha in mano un tale ce.

Vorrei infine risolvere il problema ``A MODO MIO'' per arrivare più rapidamente e con maggior incisività a determinarne la soluzione. Incomincio con l'osservare che i due archi di peso 2 sono necessariamente contenuti in ogni soluzione ottimale come dimostrano i tagli indicati in figura. (Ad esempio a pesa strettamente meno degli altri archi incidenti nel suo estremo sinistro). Ogni soluzione ottimale sarà pertanto del tipo $T= T'\cup \{a,b\}$ dove T'è un albero ricoprente minimo nel grafo ottenuto contraendo gli archi a e bcome suggerito in figura.


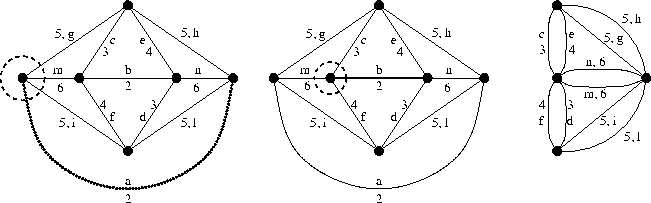
\begin{figure}% \begin{center} \leavevmode \psfig{figure=stars2.eps, height=4.5 true cm}\par\end{center}\end{figure}

Ora è evidente che i due archi di peso 4non possono essere utilizzati in alcuna soluzione ottimale dacchè ad essi preferirò sicuramente gli archi di peso 3. Ed invero, che i due archi di peso 3 erano anch'essi contenuti in ogni soluzione ottimale avrei potuto stabilirlo fin dall'inizio osservando i due tagli indicati nella prossima figura. Contraggo pertanto anche gli archi di peso 3. Ovviamente poi posso togliere i loops: non saranno contenuti in alcuna soluzione ottimale.

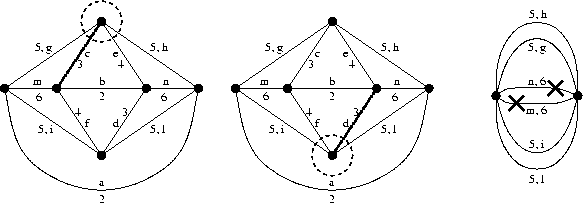
\psfig{figure=stars3.eps, height=4.5 true cm}

È ora evidente che i due archi di peso 6 non possono essere inclusi da alcuna soluzione ottimale. Una soluzione ottimale sarà pertanto del tipo $T= \{a,b,c,d\} \cup T'$dove T', albero ottimo nell'ultimo grafo rappresentato in figura, sarà costituito da uno dei seguenti quattro archi g,h,i,l. Ho pertanto 4 soluzioni ottime.

 



ESERCIZIO 2:


\begin{figure}% \begin{center} \leavevmode \psfig{figure=tria.eps, height=4.8 true cm}\par\end{center}\end{figure}

1.
Trovare un accoppiamento perfetto di peso minimo.
2.
Fornire un certificato di ottimalità.
3.
Dare tutti gli accoppiamenti perfetti di peso minimo argomentando come essi siano i soli.


Ci sono 4 accoppiamenti perfetti in tutto:
quello che contiene l'arco a, che pesa 14
quello che contiene l'arco b, che pesa 15
quello che contiene l'arco c, che pesa 15
quello che non contiene né a, né b, né c, che pesa 22.

Pertanto ho un solo accoppiamento perfetto ottimo: quello che contiene l'arco a. Una prova alla Edmonds della sua ottimalità è data dalla soluzione duale indicata in figura cui corrispondono i costi ridotti lì riportati.


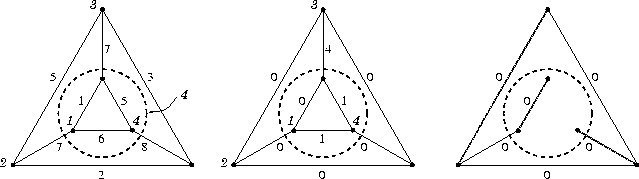
\begin{figure}% \begin{center} \leavevmode \psfig{figure=triaProve.eps, height=4 true cm}\par\end{center}\end{figure}

È poi facile verificare come negli archi a costo ridotto nullo (terzo grafo in figura), vivano solamente due accoppiamenti perfetti: quello comprendente l'arco a e quello che non contiene né a, né b, né c. Di questi due, solo il primo verifica la condizione di prendere precisamente un arco dal taglio dispari a variabile duale positiva ed indicato in figura dalla circonferenza tratteggiata. Pertanto solo l'accoppiamento comprendente l'arco a è ottimo.

 



ESERCIZIO 3:


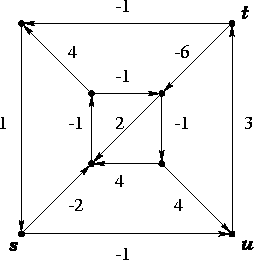
\begin{figure}% \begin{center} \leavevmode \psfig{figure=squareD.eps, height=5.8 true cm}\par\end{center}\end{figure}

1.
Trovare l'alborescenza dei cammini minimi da s.
2.
Trovare i cammini minimi da t a tutti gli altri nodi.
3.
Trovare il cammino di costo minimo da u a t.

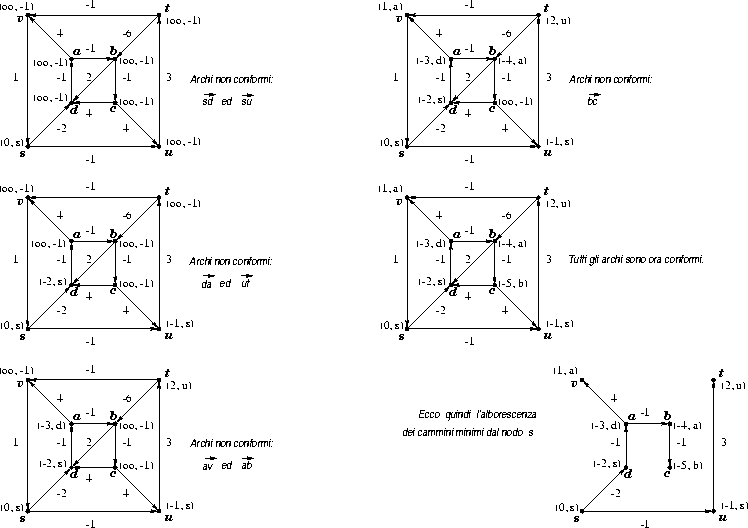
Per trovare l'alborescenza dei cammini minimi da sutilizzo l'algoritmo di Ford. Per ogni nodo devo registrare il costo del miglior cammino trovato ed il padre (nodo precedente) lungo tale cammino.


\begin{figure}% \begin{center} \leavevmode \psfig{figure=squareD1.eps, height=11.7 true cm}\par\end{center}\end{figure}

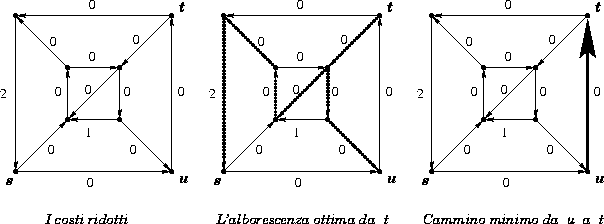
Ora che tutti gli archi sono conformi, tutti i costi ridotti saranno non negativi. Converrà pertanto cercare l'alborescenza dei cammini minimi da ted il cammino minimo da u a tnel grafo dei costi ridotti. Ecco pertanto la risposta alle ulteriori due domande.

\psfig{figure=potenziali.eps, height=5 true cm}

Esercizio 7   Quali archi posso rimuovere senza incrementare la distanza da x a y per nessuna coppia di nodi x,y?

 

ESERCIZIO 4:


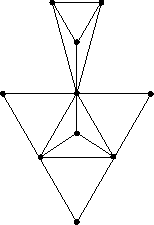
\begin{figure}% \begin{center} \leavevmode \psfig{figure=tutte.eps, height=5 true cm}\par\end{center}\end{figure}

1.
Dare un accoppiamento di cardinalità massima ed un certificato di ottimalità.
2.
Era possibile in questo caso fornire un certificato di ottimalità in termini di copertura per nodi?
3.
Si consideri l'algoritmo di Edmonds per trovare un accoppiamento di massima cardinalità. Fornire un grafo che costringa l'algoritmo a contrarre almeno un ``blossom'' e giustificare la risposta.
4.
Dare un grafo non bipartito dove la massima cardinalità di un accoppiamento pareggi la minima cardinalità di una copertura per nodi.

Un accoppiamento di cardinalità massima è dato in figura assieme ad una prova di Tutte-Berge della sua ottimalità:


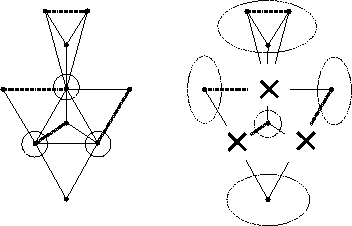
\begin{figure}% \begin{center} \leavevmode \psfig{figure=tutteProva.eps, height=5 true cm}\par\end{center}\end{figure}

Quando i 3 nodi circolettati vengono rimossi, mi ritrovo con 5 componenti dispari. Pertanto ogni accoppiamento avrà nodi esposti in almeno due delle componenti dispari sopra individuate.

Esercizio 8   Sapresti indicare tre archi che non sono contenuti in alcun accoppiamento di cardinalità massima?

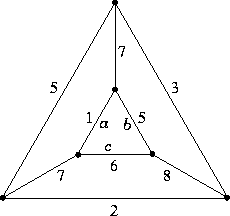
Per dimostrare che una copertura per nodi richiede almeno cinque nodi si consideri il seguente sottografo (a destra) del grafo proposto (a sinistra).


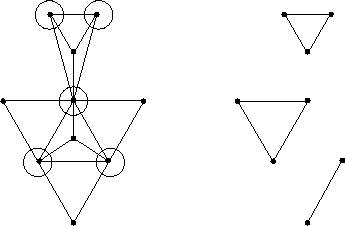
\begin{figure}% \begin{center} \leavevmode \psfig{figure=tutteCover.eps, height=5 true cm}\par\end{center}\end{figure}

Una copertura per nodi dovrà prendere almeno due nodi da ogni triangolo ed almeno un estremo dell'arco isolato. Una copertura di 5 nodi è inoltre indicata in figura.

Il grafo proposto in questo esercizio costringerà l'algoritmo di Edmonds a contrarre almeno un ``blossom'' poichè altrimenti l'algoritmo terminerebbe con una dimostrazione in termini di copertura per nodi che noi abbiamo appena dimostrato non esistere.

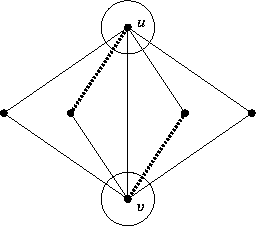
Un esempio di grafo non bipartito dove peró la cardinalità massima di un accoppiamento pareggia la cardinalità minima di una copertura per nodi é il seguente:


\begin{figure}% \begin{center} \leavevmode \psfig{figure=konig.eps, height=5 true cm}\par\end{center}\end{figure}


22 Maggio 1998 © Dipartimento di Matematica - Università di Trento