Cammini Ottimi

Problemi che richiedono di trovare il cammino di costo minimo fra una o più coppie di nodi di un grafo sono tra i più importanti nelle applicazioni pratiche. Vogliamo qui dare una panoramica introduttiva di sapore algoritmico e prettamente combinatorio.

Quando il costo di ogni arco è positivo

Dato un digrafo pesato D ed un nodo sorgente s di Dvogliamo trovare per ogni nodo $v\in V(D)\setminus\{s\}$un cammino che vada da s a v di costo minimo. (Il costo di un cammino è dato dalla somma dei pesi degli archi nel cammino).

Incominciamo con alcune facili osservazioni:

Fatto 1   L' eventuale presenza di archi privi di orientamento (archi non diretti) non costituisce un problema: un arco non orientato uv può semplicemente venir sostituito dalle frecce $\vec{uv}$ e $\vec{vu}$ come illustrato in figura.

Esercizio 2   Sapresti esprimere il contenuto di tale osservazione in modo più rigoroso, magari formulando un lemma ed eventualmente dimostrandolo?

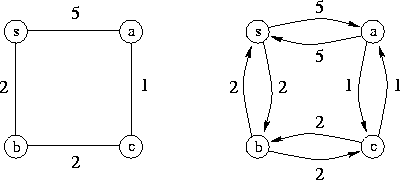
Supponiamo di essere interessati a tutti i cammini minimi da s ad ogni altro nodo. Potrebbe sembrare che in generale si andranno ad utilizzare svariati archi del grafo in esame. Invece è sempre possibile limitarsi a |V(D)|-1 archi:

Proprietà 3   Sia P_s,v un cammino minimo da s a v e sia u un qualsiasi nodo toccato da P_s,v. Allora il prefisso di P_s,v che porta da s a u è un cammino minimo da s a u. Possiamo pertanto sempre individuare un`alborescenza dei cammini minimi come illustrato in figura.

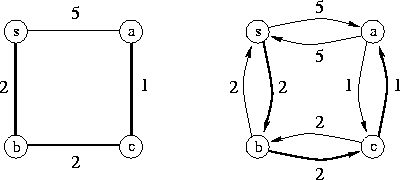
In virtù di questa osservazione ci è possibile ritornare la soluzione ottima in spazio ${\cal O}(\vert V(D)\vert)$. L'idea è la seguente: per ogni nodo v ritorno un padre $\pi(v)$ossia il penultimo nodo in un qualche cammino ottimo da s a v. Gli archi del cammino ottimo da s a v sono quindi prodotti da una procedura PATH qui sopra espressa in pseudocodice.

Pesi Tutti unitari: Breath First Search

Dato un digrafo D ed un nodo sorgente s di Dvogliamo trovare per ogni nodo $v\in V(D)\setminus\{s\}$un cammino che vada da s a v utilizzando il minor numero possibile di archi. Ci stiamo cioè restringendo al caso di cardinalità, quando tutti i pesi sono unitari.

In questo caso abbiamo un`algoritmo molto efficiente (complessità ${\cal O}(\vert E\vert)$): la famigerata Breath First Search (BFS).

Esercizio 4   Dimostrare come a terminazione sia stato trovato il cammino minimo da s ad ogni nodo raggiungibile da s.

Esercizio 5   Come implementeresti l'algoritmo per ottenere la complessità ${\cal O}(\vert E\vert)$?

Esercizio 6   L'algoritmo BFS é stato descritto utilizzando del cosidetto pseudocodice. Sapresti cogliere e puntualizzare le differenze fondamentali tra una codifica ed una pseudocodifica?

Pesi Tutti Positivi: l'algoritmo Dijkstra

Ritorniamo ora ad un caso più generale: quello pesato. Assumeremo tuttavia l'ipotesi semplificatrice che tutti i pesi siano non-negativi.

Nell'algoritmo che proponiamo le etichette che diamo ai nodi non sono sempre permanenti ossia ci riserviamo di trovare cammini migliori nel proseguio dell'algoritmo. Piú precisamente associamo un valore booleano f(v) ad ogni nodo. Quando f(v) é Falso é ancora possibile che $\lambda(v)$ diminuisca. Quando f(v) é Vero il cammino ottimo da s a v è già stato trovato.

Esercizio 7   Dimostrare come a terminazione sia stato trovato il cammino minimo da s ad ogni nodo raggiungibile da s.

Esercizio 8   Sapresti spiegare come mai non esista ancora alcuna implementazione dell'algoritmo Dijkstra con complessità ${\cal O}(\vert E\vert)$?

Tracciamo il comportamento dell' Algoritmo Dijkstra nel seguente esempio.

s	a	b	c	d	t
0	$\infty$	$\infty$	$\infty$	$\infty$	$\infty$
0	15	$\infty$	$\infty$	9	$\infty$
0	15	$\infty$	$\infty$	9	$\infty$
0	13	$\infty$	11	9	$\infty$
0	13	$\infty$	11	9	$\infty$
0	13	$\infty$	11	9	18
0	13	$\infty$	11	9	18
0	13	48	11	9	18
0	13	48	11	9	18

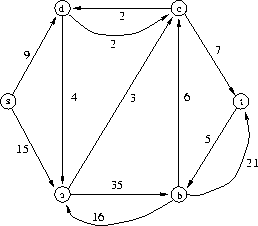
Quando non ci sono cicli negativi

Quando siamo in presenza di archi di costo negativo il problema si complica notevolmente. Tanto è vero che se non poniamo restrizione alcuna il problema di trovare un cammino semplice (nessun arco ripetuto) ottimo diviene $N\!P$-completo in quanto contiene come caso particolare il problema del cammino amiltoniano. Se non richiediamo che il cammino sia semplice allora il problema diviene illimitato se e solo se siamo in presenza di cicli negativi. Si adotta pertanto la seguente:

Assunzione 9   Il digrafo in esame non contiene alcun ciclo negativo (somma dei pesi degli archi negativa).

In virtù di tale assunzione risulta poi inessenziale richiedere o meno che i cammini siano semplici dacché ogni cammino di peso minimo eviterá di sua sponte di ciclare.

Sottolineiamo ora una questione importante: la riduzione di cui al Fatto 1 non è più applicabile poichè un arco non orientato negativo darebbe automaticamente luogo ad un ciclo negativo. Pertanto ci limiteremo ai soli digrafi.

Assunzione 10   Ogni arco del grafo in questione è una freccia.

In verità il problema di reperire i cammini minimi può essere risolto in tempo polinomiale, seppur con maggiori difficoltà, anche nel contesto di grafi ad archi non orientati e senza cicli negativi. Per fare ciò occorre utilizzare tecniche di matching o più direttamente l'algoritmo di cui ad uno degli articoli messi a disposizione in questo sito WEB.

Ritornando invece al caso più semplice dei digrafi abbiamo l'algoritmo di Ford la cui complessità è ${\cal O}(mn)$.

Esercizio 11   Dimostrare come a terminazione sia stato trovato il cammino minimo da s ad ogni nodo raggiungibile da s.

Suggerimento: Si dimostri per induzione che a completamento del ciclo a conteggio per i=k la variabile $\lambda(v)$ esprime il minimo costo di un cammino da s a v in al più k archi.

Esercizio 12   Come implementeresti l'algoritmo per ottenere la complessità ${\cal O}(\vert E\vert)$?