Contents of the first part of the LP class on December 6, 2001
We faced the problem of obtaining a first
basic feasible solution from which to start
with the simplex method.
To solve this problem,
we have introduced the auxiliary LP problem
of an LP problem in standard form.
We observed that the original problem is feasible
if and only if the optimal solution value for
the always feasible associated auxiliary problem is zero.
We have also shown how to obtain a first
basic feasible solution for the auxiliary problem.
(Together with the simplex method, this is already enough
to consent us to test the feasibility of a given set of
linear constraints).
Finally,
we have indicated how to obtain a first basic feasible
solution to the original problem (in case it is feasible)
by simply dropping the extra variable (the glue variable ![]() )
from the final
)
from the final ![]() -valued dictionary for the auxiliary problem.
Indeed, dropping a variable of value
-valued dictionary for the auxiliary problem.
Indeed, dropping a variable of value ![]() (
(![]() when the objective
function for the auxiliary problem, namely
when the objective
function for the auxiliary problem, namely ![]() equals
equals ![]() )
can not violate feasibility.
The reason why the property of ``being basic'' is also mantained
while dropping
)
can not violate feasibility.
The reason why the property of ``being basic'' is also mantained
while dropping ![]() is also due
to the fact that
is also due
to the fact that ![]() in the solution associated with this
final dictionary.
Indeed,
we have argued that we can always
act so that
in the solution associated with this
final dictionary.
Indeed,
we have argued that we can always
act so that ![]() is non-basic in this last
dictionary.
This actually means that in the so called ``Two Phases Simplex
Method''
we can, once we reach an (optimal)
is non-basic in this last
dictionary.
This actually means that in the so called ``Two Phases Simplex
Method''
we can, once we reach an (optimal) ![]() -valued
solution to the auxiliary problem,
apply right away the simplex method (second phase)
to solve the original problem,
simply discarding the column of coefficients associated to
-valued
solution to the auxiliary problem,
apply right away the simplex method (second phase)
to solve the original problem,
simply discarding the column of coefficients associated to ![]() .
.
First round of Homeworks
Solve the following LP problem by introducing the corresponding auxiliary problem and applying the Two Phases Simplex Method.
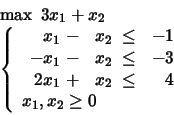
Have fun!
Contents of the second part of the LP class on Dec. 6
We have defined degeneracy
and cycling.
We have seen examples which show that under certain
(even most reasonable) pivoting rules,
cycling can actually occur.
We have considered perturbation methods
and in particular the lexicographic method
to avoid cycling.
For the lexicographic method,
we argued for its success in banning the possibility
of cycling.
We also observed that if the simplex method does not cycle
then it must terminate.
Second round of Homeworks
The Two Phases Simplex Method, implemented by employing any strategy which guarantees termination (like Bland's pivoting rule or resorting on sound perturbation methods like for example the lexicographic method) gives algorithmic proof to the following result.
Can you argue on the truth of the
Fundamental Theorem of Linear Programming
on the basis of the
Two Phases Simplex Method
and by considering its possible terminations?
Consider the following conjecture.
Which one of (i), (ii) and (iii) does still hold?
Can you provide counterexamples to the remaining properties? (Think geometrically).
With the insight gained at the previous point, can you now prove the Fundamental Theorem of Linear Programming by direct arguments, without relying on the simplex method?
If you really enjoy practicing pivot, or if you have some handy tool which can do the dirty job for you, then I dare proposing you this further exercise.
In the following LP method,
the quantity ![]() has been introduced
as a small perturbation with the porpouse
of reducing the probability of any degenearacy.
Nevertheless the simplex method will encounter
degeneracy and will actually cycle.
Can you find under which natural pivoting rules
cycling will actually occur?
has been introduced
as a small perturbation with the porpouse
of reducing the probability of any degenearacy.
Nevertheless the simplex method will encounter
degeneracy and will actually cycle.
Can you find under which natural pivoting rules
cycling will actually occur?
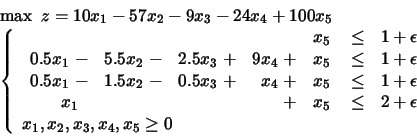
Have fun!
| 2001-12-07 |
© Dipartimento di Matematica - Università di Trento
|