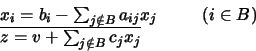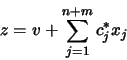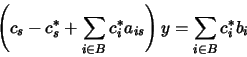ADDENDUM: Bland's pivoting rule
In 1977 R.G. Bland proposed the pivoting rule
of the least index.
When Bland's rule is adopted,
then the simplex method is guaranteed not to cycle.
Pivoting Rule 1 (Least Index Rule)
Let us assume to have introduced a total order on
the indices of the variables (hence we can regard
to the variables as to
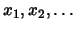
).
- When more non-basic variables are candidates for entering the basis
(positive reduced cost),
then we choose among them the variable of smallest index.
- When more basic variables are candidates for leaving the basis
(hence degeneracy will result, since even the ones among them which
will remain basic will have
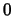 value in the basic solution
associated to the next dictionary),
then we choose among them the variable of smallest index.
value in the basic solution
associated to the next dictionary),
then we choose among them the variable of smallest index.
Note that Bland's rule uniquely specifies
both the entering and the leaving variable
(contrary to what happens with the anti-degenerative
methods like the perturbation method or the lexicographic method,
where only the exiting variable is decided by the method
and we are left free choice on the entering variable).
In fact, this drawback delayed (at least in a first time)
its adoption.
Here follows a formal proof of the following result.
Teorema 1 (R. G. Bland 1977)
When the least index rule is adopted,
then the simplex method can not cycle.
(And hence its termination is guaranteed).
proof:
Assume, by absurd,
that the method cycles producing the following
sequence of dictionaries:
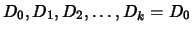 .
A variable is called fickle
if it is basic for some but not all of these dictionaries.
Let
.
A variable is called fickle
if it is basic for some but not all of these dictionaries.
Let 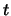 be the maximum index for which
be the maximum index for which 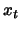 is fickle.
In the sequence
is fickle.
In the sequence
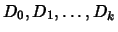 there will be a dictionary
there will be a dictionary 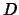 having
having 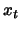 as exiting variable
(basic for
as exiting variable
(basic for 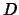 but non-basic for the next dictionary)
and let
but non-basic for the next dictionary)
and let 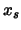 be the variable entering in the basis
in place of
be the variable entering in the basis
in place of 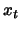 .
Clearly, the sequence
.
Clearly, the sequence
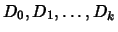 contains a dictionary
contains a dictionary 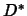 with
with 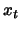 entering back.
Where
entering back.
Where 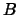 is the set of indices
of the variables which are basic for
is the set of indices
of the variables which are basic for 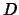 ,
then the structure of
,
then the structure of 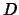 is as follows:
is as follows:
Moreover, the objective function 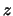 takes
the same value in the basic solutions associated
to
takes
the same value in the basic solutions associated
to 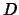 and
and 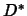 .
Therefore, last row of dictionary
.
Therefore, last row of dictionary 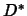 can be written as:
can be written as:
where 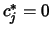 whenever
whenever 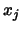 is basic for
is basic for 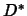 .
Since this last equation has been obtained
from the equations describing
.
Since this last equation has been obtained
from the equations describing 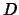 through pivoting
operations, it must admit any solution which is admitted from
through pivoting
operations, it must admit any solution which is admitted from 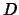 .
In particular,
it must be satisfied by the following choice of values:
.
In particular,
it must be satisfied by the following choice of values:
Therefore,
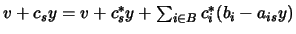 ,
which, after simple rewriting becomes:
,
which, after simple rewriting becomes:
Since the second term of this equation is a constant
independent from 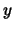 we can conclude that
we can conclude that
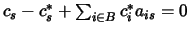 .
Moreover,
.
Moreover, 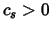 since
since 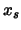 is entering in
is entering in  .
Furthermore
.
Furthermore 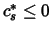 since
since 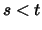 and nevertheless
and nevertheless
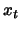 and not
and not 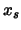 is the variable entering in
is the variable entering in 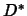 .
We therefore conclude that
.
We therefore conclude that
Since 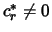 , the variable
, the variable 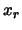 is not basic
for
is not basic
for 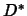 and is hence fickle.
However
and is hence fickle.
However 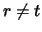 since
since
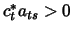 :
since
:
since 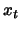 enters for
enters for 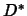 , then
, then 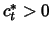 ;
since
;
since 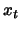 exits for
exits for 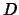 , then
, then 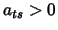 .
Therefore,
.
Therefore, 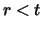 and since
and since 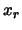 does not enter in
does not enter in 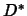 in the place of
in the place of 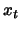 , we can conclude that
, we can conclude that 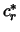 can not be positive.
Therefore
can not be positive.
Therefore
Since all iterations in the cycle are degenerate,
to 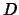 and
and 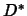 precisely the same solution is associated.
And all fickle variables are set to zero in this solution.
In particular
precisely the same solution is associated.
And all fickle variables are set to zero in this solution.
In particular 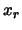 , which is non-basic for
, which is non-basic for 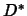 ,
will have zero value also in the solution
associated to
,
will have zero value also in the solution
associated to 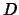 and therefore
and therefore 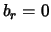 .
But then
.
But then 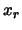 was a candidate to leave the basis in
was a candidate to leave the basis in 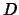 .
This is at odds with the least index rule,
since we preferred
.
This is at odds with the least index rule,
since we preferred 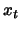 to
to 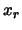 .
.

|
2001-12-07
|
© Dipartimento di Matematica - Università di Trento
|
 value in the basic solution
associated to the next dictionary),
then we choose among them the variable of smallest index.
value in the basic solution
associated to the next dictionary),
then we choose among them the variable of smallest index.