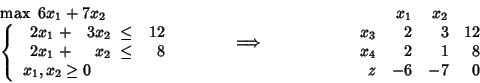
La lettura di questo documento è strettamente
consigliata agli studenti che intendano affrontare la
provetta di Programmazione Lineare.
Svolgeremo quì di seguito alcuni
esercizi di preparazione alla provetta.
Ci atterremo a procedimenti standard di soluzione.
Proporremo inoltre l'uso del tableau.
Il tableau si è imposto come scrittura compatta di
un dizionario nella didattica della
Programmazione Lineare.
Spesso i vari elementi,
teorici ed algoritmici,
che compongono la PL
vengono introdotti come metodi
di manipolazione del tableau che conducano
ai risultati desiderati.
Se avrete altre occasioni di incontro con la PL
vi dovrete probabilmente confrontare
con il tableau.
Conviene pertanto impadronirsi ora di questo approccio
con relativo linguaggio e tecnicalità.
E comunque la conoscenza del tableau
come descritto in questo documento è intesa
come parte integrante del programma del corso.
Per quanto riguarda la provetta l'uso del tableau
non è nè obbligatorio nè incoraggiato.
Tuttavia esso è consigliato
dacchè
il presentare i passaggi in forma compatta
aumenta chiarezza e leggibilità.
In pratica il tableau offre lo strumento,
di fatto standard,
per incrementare la qualità del documento prodotto
nello svolgimento di problemi di PL.
Buona Lettura.
Il tableau ed il metodo del simplesso
Al seguente problema di PL associo il corrispondente tableau:
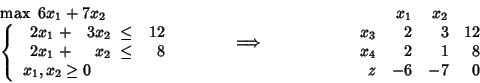
Dove ![]() ed
ed ![]() indicano le variabili di slack.
Osserviamo che i coefficienti della funzione obiettivo
(o costi) vengono riportati nel tableau col segno rovesciato
e che alla funzione obiettivo corrisponde
(nella prassi diffusa)
l'ultima riga.
indicano le variabili di slack.
Osserviamo che i coefficienti della funzione obiettivo
(o costi) vengono riportati nel tableau col segno rovesciato
e che alla funzione obiettivo corrisponde
(nella prassi diffusa)
l'ultima riga.
A dire il vero il tableau non corrisponde propriamente ad un problema di PL ma ad un particolare dizionario di un problema di PL ossia ad un problema di PL visto dalla particolare prospettiva di una sua soluzione di base (ammissibile o meno). Il caso di cui sopra era fortuito: essendo il problema in forma standard era possibile scriverne direttamente un primo tableau.
In corrispondenza di una qualsiasi soluzione,
la funzione obiettivo assume un determinato valore,
che viene riportato a destra nell'ultima riga del tableau.
In generale, il seguente dizionario è più compattamente descritto in forma di tableau:
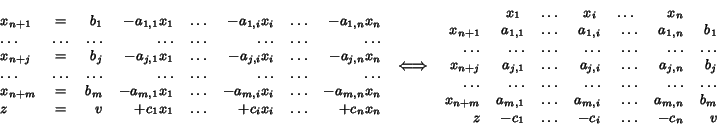
Ecco un secondo esempio:


La scelta della riga di pivot si effettua
considerando tutti gli
![]() positivi.
Tra questi, quello che minimizza il rapporto
positivi.
Tra questi, quello che minimizza il rapporto
![]() ,
è l'elemento di pivot.
,
è l'elemento di pivot.
Eseguiamo ora il passo di pivot nel dizionario e scopriamo così come debba venir aggiornato il tableau.
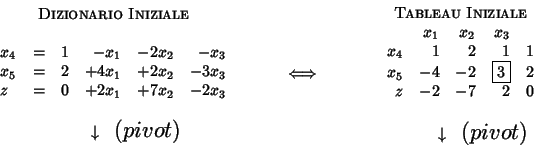
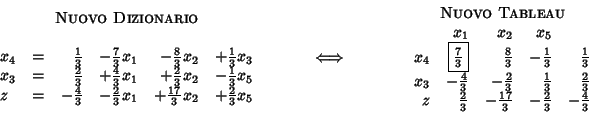
Nel tableau, siano ![]() e
e ![]() la riga e la colonna di pivot.
Sia
la riga e la colonna di pivot.
Sia
![]() il valore dell'elemento di pivot.
Ecco la regola generale per
eseguire il pivot direttamente sul tableau:
il valore dell'elemento di pivot.
Ecco la regola generale per
eseguire il pivot direttamente sul tableau:
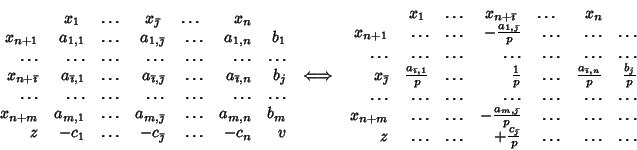
Abbiamo cioè il seguente meccanismo di pivot.
L'operazione di pivot è forse meglio illustrata in Figura 1.
Ma ritorniamo al nostro problema di PL ed eseguiamo il prossimo passo di pivot.

Gli elementi dell'ultima riga
sono ora tutti negativi.
Possiamo pertanto concludere che il valore ottimo del nostro
problema era ![]() .
(Perchè?)
La soluzione primale ottima è
.
(Perchè?)
La soluzione primale ottima è
![]() con
con
![]() e
e
![]() .
La soluzione duale ottima è
.
La soluzione duale ottima è ![]() con
con
![]() ,
,
![]() e
e
![]() ed è anch'essa espressa nel tableau.
ed è anch'essa espressa nel tableau.
Di fatto è persino possibile ricavare il tableau del problema duale dal tableau del problema primale.
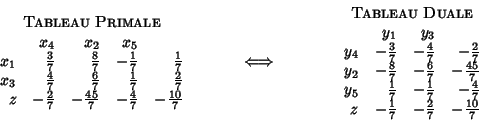
Dove la variabile duale ![]() corrisponde alla variabile
di slack
corrisponde alla variabile
di slack ![]() e cioè è il moltiplicatore del primo vincolo.
La variabile duale
e cioè è il moltiplicatore del primo vincolo.
La variabile duale ![]() corrisponde alla variabile
primale
corrisponde alla variabile
primale ![]() che è il moltiplicatore del primo vincolo duale,
ossia
che è il moltiplicatore del primo vincolo duale,
ossia ![]() è la variabile di surplus nel primo vincolo duale.
è la variabile di surplus nel primo vincolo duale.
Qualora si debba massimizzare la funzione obiettivo
allora seguiamo la stessa procedura,
solo che ora miriamo ad ottenere valori non negativi nell'ultima riga.
Ad esempio:
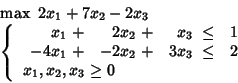
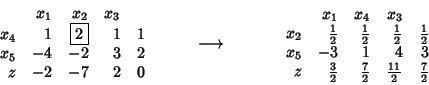
Il valore ottimo della funzione obiettivo è ora ![]() .
La soluzione primale ottima è
.
La soluzione primale ottima è ![]() con
con
![]() .
La soluzione duale ottima è
.
La soluzione duale ottima è
![]() con
con
![]() .
.
|
LA PROVA DI CONTROLLO Anche la PL ha la sua prova del nove. Si assegni ad ogni variabile il valore del coefficiente di quella variabile nella funzione obiettivo originaria. Ad esempio l'ultimo tableau diviene:
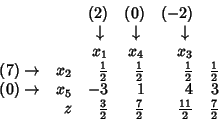
Per ogni colonna vale quanto segue:
il valore del coefficiente associato alla colonna
più il valore dell'ultimo elemento della colonna
eguaglia la somma degli altri elementi della colonna ciascuno
moltiplicato per il coefficiente della riga cui appartiene.
Colonna 1:
Queste relazioni valgono per ogni tableau, non necessariamente ottimale.
|
Il tableau ed il metodo del simplesso duale
Consideriamo un problema in forma standard e si assuma per fissare le idee che esso sia un problema di massimizzazione. Si assuma inoltre che tutti i coefficienti della funzione obiettivo siano non-positivi. Pertanto nel primo tableau i coefficienti nell'ultima riga sono di già non-negativi, come li vorremmo nell'ultimo tableau. Un tale tableau è detto duale ammissibile. Se poi tutti i coefficienti nell'ultima colonna sono non-negativi allora la soluzione di base corrente è ammissibile ed il problema è già risolto. Altrimenti si applica il metodo del simplesso duale. Una caratteristica interessante del metodo del simplesso duale sul tableau è che l'operazione di pivot si esplica esattamente come la regola di pivot per il simplesso primale. L'unica differenza operativa tra i due metodi stà nella scelta dell'elemento di pivot che nel caso del simplesso duale segue la stessa filosofia già richiamata per il simplesso primale.
La scelta della colonna di pivot si effettua
considerando tutti gli
![]() negativi.
Tra questi, quello che minimizza il rapporto
negativi.
Tra questi, quello che minimizza il rapporto
![]() ,
è l'elemento di pivot.
,
è l'elemento di pivot.
Ecco un esempio:
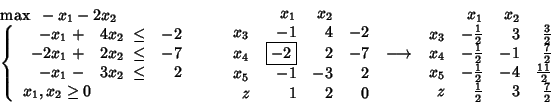
Come gestire i vincoli sulle singole variabili
Se invece di avere ![]() si ha
si ha ![]() con
con ![]() allora ci si avvale della sostituzione:
allora ci si avvale della sostituzione:
![]() .
Se poi una variabile è limitata verso il basso
invece che verso l'alto,
ossia
.
Se poi una variabile è limitata verso il basso
invece che verso l'alto,
ossia ![]() ,
ma
,
ma ![]() non è richiesto,
allora si sostituisce
non è richiesto,
allora si sostituisce
![]() .
.
Qualora invece una variabile non-negativa
sia limitata verso il basso,
tale condizione può essere considerata
come uno dei vincoli del problema.
Tuttavia, qualora tutte le variabili siano limitate
(ed in molti casi un limite ovvio è facilmente prodotto),
allora la situazione può essere girata a nostro vantaggio
considerando sia la variabile ![]() che
la variabile
che
la variabile
![]() e decidendo di adottare per la scrittura
del primo tableau quella delle due che
conduce ad un tableau duale ammissibile.
Si procede quindi con il metodo del simplesso duale.
Dobbiamo ovviamente garantire
e decidendo di adottare per la scrittura
del primo tableau quella delle due che
conduce ad un tableau duale ammissibile.
Si procede quindi con il metodo del simplesso duale.
Dobbiamo ovviamente garantire
![]() .
Attraverso le varie fasi del simplesso duale
l'ammissibilità duale resta garantita,
e se una delle variabili primali utilizzate per esprimere
il tableau (
.
Attraverso le varie fasi del simplesso duale
l'ammissibilità duale resta garantita,
e se una delle variabili primali utilizzate per esprimere
il tableau (![]() o
o ![]() ) è negativa allora
un passo di pivot viene eseguito con l'effetto
di avvicinarsi all'ammissibilità anche primale.
Tuttavia può accadere che una variabile attualmente
presente nel tableau ecceda il suo limite verso il basso.
Quando ciò succede si rimpiazza la rispettiva riga del tableau:
) è negativa allora
un passo di pivot viene eseguito con l'effetto
di avvicinarsi all'ammissibilità anche primale.
Tuttavia può accadere che una variabile attualmente
presente nel tableau ecceda il suo limite verso il basso.
Quando ciò succede si rimpiazza la rispettiva riga del tableau:
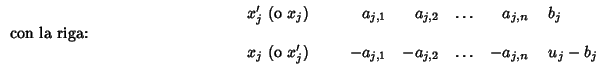
e proseguendo. Ad esempio:
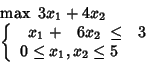
Introdotte le variabili
![]() ed
ed
![]() si sceglie di utilizzare nel tableau
proprio
si sceglie di utilizzare nel tableau
proprio ![]() ed
ed ![]() dacchè
i coefficienti della funzione obiettivo erano
entrambi positivi (e quindi?).
dacchè
i coefficienti della funzione obiettivo erano
entrambi positivi (e quindi?).
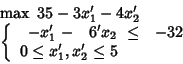
La sequenza dei tableau è quindi:
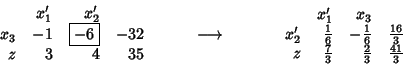
Ora
![]() e pertanto la prima riga del
tableau viene sostituita introducendo
e pertanto la prima riga del
tableau viene sostituita introducendo ![]() :
:
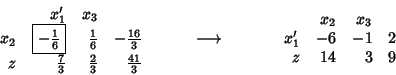
Soluzione ottima: ![]() ed
ed ![]() con funzione obiettivo
con funzione obiettivo ![]() .
.
Analisi di Sensitività
Supponiamo di massimizzare una funzione obiettivo
che rappresenti un profitto o qualche altra forma
di beneficio.
I vincoli descriveranno limitazioni
in materie prime o disponibilità.
Allora i valori delle variabili duali
esprimeranno il massimo ``prezzo''
che saremmo disposti a pagare per incrementare
di un'unità la disponibilità cui la variabile
duale si riferisce.
(Da qui il nome di ``prezzo ombra'' o ``valore marginale'').
Ricordiamo che tuttavia il significato di un prezzo
ombra è strettamente locale e che in generale
non sarà conveniente continuare a pagare sulla
base del prezzo ombra per un incremento comunque grande
di disponibilità.
Ci chiediamo ora fino a dove il prezzo ombra
é significativo
ossia quale sia il massimo incremento
di una certa facilità
che ha senso promuovere pagando il prezzo ombra.
La risposta può essere prodotta agevolmente
con riferimento al tableau duale.
Si consideri ad esempio di voler massimizzare il seguente profitto:
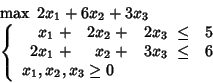
dove ![]() ed
ed ![]() esprimono dei livelli non-negativi di attività,
mentre i coefficienti di destra nei vincoli
impongono limiti su determinate disponibilità.
Il tableau associato alla soluzione di base ottimale é il seguente.
esprimono dei livelli non-negativi di attività,
mentre i coefficienti di destra nei vincoli
impongono limiti su determinate disponibilità.
Il tableau associato alla soluzione di base ottimale é il seguente.

Pertanto saremmo disposti a pagare (non certo più di ) ![]() per incrementare di un'unità la disponibilità
nel primo vincolo.
Ma quanto siamo disposti a comperare?
Si consideri il duale dell'ultimo tableau:
per incrementare di un'unità la disponibilità
nel primo vincolo.
Ma quanto siamo disposti a comperare?
Si consideri il duale dell'ultimo tableau:
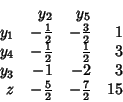
Assumiamo di incrementare di ![]() la disponibilità nel primo vincolo.
Il vantaggio nel considerare il duale é
che l'unica riga ad essere influenzata da questa
modifica nel problema è l'ultima.
La nuova riga può essere prodotta
attraverso opportune sostituzioni o
avvalendosi della PROVA DI CONTROLLO (prova del nove) della PL.
la disponibilità nel primo vincolo.
Il vantaggio nel considerare il duale é
che l'unica riga ad essere influenzata da questa
modifica nel problema è l'ultima.
La nuova riga può essere prodotta
attraverso opportune sostituzioni o
avvalendosi della PROVA DI CONTROLLO (prova del nove) della PL.
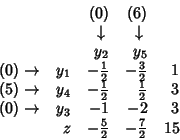
Ricordiamo che per ogni colonna vale quanto segue:
il valore dell'ultimo elemento della colonna
si ottiene sommando gli altri elementi della colonna ciascuno
moltiplicato per il coefficiente della riga cui appartiene
e sottraendo infine il valore del coefficiente associato alla colonna.
Colonna 1:
![]()
Colonna 2:
![]()
Colonna 3:
![]()
Pertanto la riga prodotta è:
Pertanto il tableau resta ottimo fintanto chè
![]() non supera
non supera ![]() .
Concludendo
.
Concludendo ![]() è il massimo incremento di diponibilità
nel primo vincolo che siamo disposti ad acquistare
pagando
è il massimo incremento di diponibilità
nel primo vincolo che siamo disposti ad acquistare
pagando ![]() per ogni unità di incremento.
Per determinare il prezzo
che siamo disposti a pagare per incrementi superiori
(il nuovo prezzo ombra)
dobbiamo eseguire un nuovo pivot.
per ogni unità di incremento.
Per determinare il prezzo
che siamo disposti a pagare per incrementi superiori
(il nuovo prezzo ombra)
dobbiamo eseguire un nuovo pivot.
| 2001-12-19 |
© Dipartimento di Matematica - Università di Trento
|