Possiamo esprimere in una forma chiusa ed esatta

il numero di confronti impiegati da MergeSort

secondo il criterio del caso peggiore?

Come primo esempio della tecnica divide et impera, abbiamo considerato l'algoritmo per l'ordinamento comunemente chiamato MergeSort. Era questo un algoritmo ricorsivo (trovi il codice tra le pagine web del corso) che per ordinare $n$ elementi chiamava se stesso su $\left\lceil \frac{n}{2} \right\rceil$ degli elementi da un lato, e sui restanti $\left\lfloor \frac{n}{2} \right\rfloor$ dall'altro, ed infine invocava una sottoprocedura, chiamata Merge, il cui ruolo era quello di combinare in un'unica lista ordinata gli $n$ elementi di due liste ordinate, di $\left\lceil \frac{n}{2} \right\rceil$ ed $\left\lfloor \frac{n}{2} \right\rfloor$ elementi rispettivamente. Il numero di confronti impiegato dalla sottoprocedura Merge era $n-1$, nel caso peggiore.

Solo per richiamarvi il contesto di riferimento, potete provare a porvi la seguente domanda.

Domanda 1   Poteva la nostra Merge impiegare meno di $n-1$ confronti, a seconda delle sequenze ricevure in input?

Inoltre, tra le pagine web del corso, trovate parziali risposte alla seguente domanda, che inquieta le notti della nostra procedura Merge.

Domanda 2   Quale è il minimo numero di confronti che un qualsiasi algoritmo dovrà impiegare nel suo caso peggiore per fare il merging di due liste ordinate?

Ma lo scopo di questa dispensa è l'affrontare assieme la seguente domanda.

Domanda 3   Quale è il massimo numero di confronti che MergeSort sarà chiamato ad eseguire nell'ordinare una sequenza di $n$ numeri?

Si indichi pertanto con $T_n$ il massimo numero di confronti che MergeSort sarà chiamato ad eseguire nell'ordinare una sequenza di $n$ numeri.

Check Please 1   Possiamo scrivere la seguente ricorrenza, vero?

$$T_n = T_{\left\lceil \frac{n}{2} \right\rceil} + T_{\left\... ...loor} + n-1 \mbox{\hspace{1cm} per $n\geq 2$, con $T_1 = 0$.}$$ (1)

Ad onor del vero, avevamo già fornito alcune risposte parziali alla Domanda 3. Ad esempio, ragionando in termini di alberi dei confronti, avevamo visto che tali alberi binari dovevano avere altezza almeno $\left\lceil \log_2 n! \right\rceil$, e ne avevamo concluso che un qualsiasi algoritmo di ordinamento basato sul confronto si ritrovava costretto a compiere almeno $\left\lceil \log_2 n! \right\rceil = n\log_2 n - O(n)$ confronti nel caso peggiore. Ne consegue che $T_n \geq n\log_2 n - O(n)$, dacchè MergeSort non potrà costituire eccezzione.

Domanda 4   A lezione, avevamo inoltre visto che il tempo di calcolo per l'algoritmo MergeSort era $O(n\log n)$. Possiamo concludere che $T_n = O(n\log n)$? Possiamo concludere che $T_n = \Theta(n\log n)$?

Domanda 5   Secondo te, per quale motivo abbiamo specificato la base del logaritmo nella scrittura $T_n \geq n\log_2 n - O(n)$ ma ci siamo dimenticati di farlo nella scritura $T_n = O(n\log n)$?
In base a quanto sopra detto, possiamo concludere che $T_n \leq n\log_2 n$? Possiamo concludere che $T_n \leq n\log_b n$ per un qualche $b>0$?

Esercizio 1   Scrivete in 5 righe di c++ un semplice programma iterativo (ad esempio riadattando il programma c++ iterativo per determinare il maggior numero di confronti impiegati dalla binary search su $n$ elementi, codici disponibili tra le pagine web del corso) che vi consenta di tabulare efficacemente i valori di $T_n$ per $n\leq 250$. Usare quindi GNUPLOT per tracciare il grafico di $T_n$. Cosa vien fuori? Vien fuori una funzione continua e regolare? Se sì, allora vuol dire che questo è davvero un caso fortunato. Non ce lo saremmo davvero aspettato visti gli arrotondamenti verso l'alto e verso il basso presenti nella ricorrenza.

Se siamo così fortunati, se la funzione $T_n$ ci appare regolare, allora forse abbiamo qualche speranza di trovare una semplice forma chiusa che esprima $T_n$ in modo esatto. Ma prima di procedere, e solo per rendersi conto della fortuna avuta, si completi e compendi l'esercizio sopra con il seguente.

Esercizio 2   Scrivete un semplice programma c++ iterativo (riadattare una linea del codice c++ di cui ad esercizio precedente) per tabulare efficacemente, per $n\leq 250$, i valori di $T'_n$ definita come

$$T'_n = T'_{\left\lceil \frac{n}{2} \right\rceil} +T'_{\lef... ...\rceil} + n-1 \mbox{\hspace{1cm} per $n>1$, con $T'_1 = 0$.}$$

Usare quindi GNUPLOT per tracciare il grafico di $T'_n$. Cosa vien fuori? Vien fuori una funzione continua e regolare? Se sì, allora vuol dire che questo è davvero un caso fortunato. Non ce lo saremmo davvero aspettato visti gli arrotondamenti presenti nella ricorrenza.

Domanda 6   Vi sarete chiesti: ``Ma visto che una ricorrenza è per sua natura una cosa ricorsiva, perchè allora negli esercizi sopra ci viene suggerito di scrivere dei programmini c++ iterativi?''

Ebbene, la ragione c'è ed è molto importante, delicata, ed interessante. Se non vi riesce ancora di coglierla (è anche sottile), provate allora a scrivere sia un codice iterativo che uno ricorsivo per la tabulazione della ricorrenza

$$F_n = F_{n-1} + F_{n-2} \mbox{\hspace{1cm} per $n>1$, con $F_0 = 0, F_1 = 1$.}$$

(Si tratta della ricorrenza che definisce i numeri di Fibonacci, e trovi almeno il codice iterativo tra le pagine del corso). Dopo aver verificato che i due codici siano entrambi corretti, verificando le risposte dell'uno contro le risposte dell'altro per piccoli valori di $n$, scegli il tipo LONG LONG INT per le varibili intere, per apprestarti a valutare la tenuta dei tuoi codici per $n$ più grandino. Quanto ci mette l'algoritmo iterativo a computare $F_{50}$? Riuscirà mai l'algoritmo ricorsivo a computarti $F_{50}$? Se sì, quanto stimi ci possa mettere?

Attenzione!!! 1   Prima di proseguire con la lettura del presente documento, sarebbe bene aveste sperimentato e digerito le proposte di lavoro fin qui avanzate.

Va bene, ci siamo accorti sperimentalmente che l'andamento di $T_n$ è regolare e questo ci fa ben sperare di riuscire ad ottenere un' espressione esplicita per $T_n$ in forma chiusa. A questo scopo consigliamo di differenziare la ricorrenza 1, ossia di ricavare da essa la ricorrenza che definisca la quantità $D_n := T_{n+1} - T_n$. Otterremo così una ricorrenza più semplice, la soluzione della quale comporterà automaticamente la soluzione della ricorrenza originaria.

$$D_n = D_{\left\lfloor \frac{n}{2} \right\rfloor} + 1 \mbox{\hspace{1cm} per $n\geq 2$, con $D_1 = 1$.}$$ (2)

Esercizio 3   Cerca con le tue mani di ricavare la ricorrenza 2 a partire dalla ricorrenza 1.

Esercizio 4   Riadattare il programmino c++ per la tabulazione della $T_n$ affinchè tabuli anche la $D_n$. Tale programmino potrebbe anche essere impiegato per verificare che la ricorrenza 2 definisca correttamente la quantità $D_n := T_{n+1} - T_n$.

Esercizio 5   Risolvi la ricorrenza 2, ossia trova l'espressione esplicita per la quantità $D_n := T_{n+1} - T_n$. (Suggerimento: se avrai affrontato l'esercizio 4 quì sopra non credo che troverai difficoltà insormontabili).

Attenzione!!! 2   Prima di proseguire con la lettura del presente documento, sarebbe bene aveste sperimentato e digerito le proposte di lavoro fin qui avanzate.

E tuttavia vogliamo ora proporre in questa occasione un ulteriore modo di andare a risolvere ricorrenze: quello di andare a capirle nella loro natura e riconoscerle.

Esercizio 6   Si consideri il numero di confronti $C_n$ impiegato nel caso peggiore durante una ricerca binaria con mancato reperimento (la chiave cercata non era presente nell'array ordinato) su un array di $n$ elementi. Si scriva la ricorrenza che descrive $C_n$. La si confronti con la ricorrenza che descrive $D_n$.

Ora, se le ricorrenze per $C_n$ e $D_n$ fossero anche solo simili, ciò potrebbe portare alla soluzione della ricorrenza per $D_n$ qualora la soluzione per $C_n$ fosse già presente nel mio repertorio. Di fatto questo approccio alla soluzione delle ricorrenze prende il nome di metodo del repertorio. Potrà a prima vista sembrare un approccio poco soddisfacente, ma a ben vedere, come anche in altri contesti, non possiamo sminuire importanza e ruolo dell'arte di collegare un nuovo problema a problemi già incontrati e classificati vuoi nel bene (classificati come risolti) come nel male (rimasti irrisolti o dimostrati irrisolvibili, almeno in una qualche ben definita accezzione). Non vorremmo infatti nè continuare a reinventare ettolitri su ettolitri di acqua calda, nè perdere il nostro tempo su una ricorrenza sostanzialmente equivalente ad una famigerata ricorrenza su cui hanno misurato insuccessi, od hanno già determinato risposte negative, i grandi matematici che ci hanno preceduto. Nel caso delle ricorrenze poi, guardare ad una stessa ricorrenza da più punti di vista può condurci in semplicità alla soluzione. Anche gli alpinisti più audaci scelgono prima la parate da cui converrà tentare la scalata.

Nel seguente esercizio, ci permettiamo di indicare una via interessante.

Esercizio 7   Si consideri il numero minimo di cifre binarie $B_n$ necessarie alla codifica del numero naturale $n$. In pratica, $B_n$ esprimerà il numero di bits nella rappresentazione binaria di $n$, con l'assunzione di ignorare gli zeri posti a sinistra. (Pertanto, $B_0=0$). su un array di $n$ elementi. Si scriva una ricorrenza che descriva $B_n$, considerato che se togliamo il bit di destra dalla rappresentazione di $n$ otteniamo la rappresentazione di $\lfloor \log_2 n \rfloor +1$. Si confronti la ricorrenza ottenuta con le ricorrenze che descrivono $C_n$ e $D_n$.

Teorema 1   La ricorrenza 2 ha soluzione esatta $D_n = \lfloor \log_2 n \rfloor +1$.

Dimostrazione: Se hai eseguito gli esercizi proposti, avrai scoperto che $D_n = C_n =B_n$. Vogliamo seguire il suggerimento, ed affrontare la scalata dalla parete $B_n$.

Se ignoriamo gli zeri posti a sinistra, il numero di bits nella rappresentazione binaria di $n$ è $t$ per $2^{t-1} \leq n < 2^t$, ossia, prendendo il logaritmo, per $t-1\leq \log_2 n < t$. In definitiva, $t-1 = \lfloor \log_2 n \rfloor$ e quindi $t = \lfloor \log_2 n \rfloor +1$.

Esercizio 8   Se hai provato a dimostrare che $D_n = \lfloor \log_2 n \rfloor +1$ per induzione, avrai probabilmente dovuto superare numerose difficoltà lungo il tuo cammino. (Provare per credere). Un interessante approccio alternativo sarebbe stato quello di dimostrare, per induzione, che $t\in [2^{D_t -1}, \ldots, 2^{D_t} -1]$ per ogni naturale $t$. Vuoi provare?

Attenzione!!! 3   Prima di proseguire con la lettura del presente documento, sarebbe bene aveste sperimentato e digerito le proposte di lavoro fin qui avanzate.

Avendo trovato una forma chiusa ed esatta per la quantità $D_n := T_{n+1} - T_n$, dovremmo ora essere in grado di ricostruire la soluzione esatta per la $T_n$.

Esercizio 9   Dove, $D_n = \lfloor \log_2 n \rfloor +1$, si risolva la seguente ricorrenze per semplice iterazione.

$$T_{n+1} = T_n + D_n$$

Cosa vuol dire risolvere una ricorrenza per iterazione? Beh, proviamo ad applicare iterativamente la definizione della ricorrenza.

$$T_{n+1} = D_n + T_n = D_n + D_{n-1} + T_{n-1} = \ldots = D... ... \ldots + D_1 + T_1 = \sum_{i=1}^n D_i + 0 = \sum_{i=1}^n D_i$$

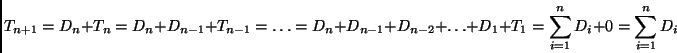
Non ci deve sorprendere la facilità con cui abbiamo saputo iterare in questo caso, in fondo la quantità $T$ appariva una sola volta sul lato destro della ricorsione, e quindi non avevo diramazioni da gestire.

Sacro Grahal 1   Ricercare esempi, meglio se classici o notevoli, ove il metodo dell'iterazione si applichi con successo nonostante ci siano diramazioni, ossia la quantità di interesse compaia più volte sul lato destro della ricorrenza.

La discussione di cui sopra conduce al seguente risultato.

Teorema 2   Il numero di confronti impiegato da MergeSort nel caso peggiore (sull'istanza più avversa di $n$ elementi) è dato dal numero di bits necessario al rappresentare tutti i naturali minori di $n$.

Dimostrazione: Abbiamo infatti visto che

$$T_n = \sum_{i=1}^{n-1} D_i = \sum_{i=1}^{n-1} B_i$$

Vorremmo però un' espressione, magari meno magica, ma più esplicita.

Teorema 3   Il numero di confronti impiegato da MergeSort nel caso peggiore è dato da $T_n=n{\lfloor \log_2 n \rfloor}+n - 2^{{\lfloor \log_2 n \rfloor} +1} +1$.

Dimostrazione: Abbiamo già visto che

$$T_n = \sum_{i=1}^{n-1} B_i$$

Ora, tutti gli $n-1$ interi positivi inferiori ad $n$ contribuiscono alla sommatoria con un bit di destra (bit meno significativo); in aggiunta, $n-2$ di essi contribuiscono alla sommatoria con un secondo bit (un bit in seconda posizione); in aggiunta, $n-4$ di essi contribuiscono alla sommatoria con un terzo bit (un bit in terza posizione); e così via ... . Pertanto

$$\begin{eqnarray*} T_n &=& (n-1)+(n-2)+(n-4)+(n-8) + \ldots +(n-2^{\lfloor \log... ...floor \log_2 n \rfloor}+n - 2^{{\lfloor \log_2 n \rfloor} +1} +1 \end{eqnarray*}$$

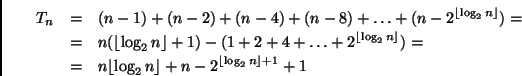
Ovviamente, ${\lfloor \log_2 n \rfloor}$ è una funzione discontinua. Chi di voi aveva però tabulato la $T_n$, aveva invece avuto modo di osservare un andamento continuo. Deve pertanto accadere che i contributi delle due funzioni della quantità discontinua ${\lfloor \log_2 n \rfloor}$ nell'espressione della $T_n$ si elidano a vicenda. Essendo a conoscenza di questa cancellazione, ùn' operazione di routine mettere in evidenza questo fatto, e pervenire ad una forma analitica ancor più soddisfacente. A tale scopo, indicata con $\{\log_2 n\} := \log_2 n -{\lfloor \log_2 n \rfloor}$ la parte frazionaria di $\log_2 n$, si sostituisca fuori la grandezza ${\lfloor \log_2 n \rfloor}$ eliminandola dall'espressione di $T_n$. Ciò dovrebbe condurre al seguente risultato.

Corollario 4   Il numero di confronti impiegato da MergeSort nel caso peggiore è dato da $T_n=n\log_2 n -n +n\theta(1- \{\log_2 n\}) +1$, dove $\theta(x)=1+x-2^x$ è una funzione mai negativa che soddisfa $\theta(0)=\theta(1)=0$ e $0<\theta(x)< 0.086$ per $0<x<1$.

Dimostrazione: Nell' espressione per $T_n$ ottenuta precedentemente, si sostituisca ${\lfloor \log_2 n \rfloor}$ con $\log_2 n - \{\log_2 n\}$. Il valore $0.086 \equiv 1-\log e + \log \log e$ è ottenuto ponendo la derivata di $\theta(x)$ a zero.