


Next: About this document ...
Qual è il minimo numero di confronti
che garantisca il merge di 2 liste ordinate?
In seno all'algoritmo per l'ordinamento
chiamato MergeSort abbiamo incontrato
una sottoprocedura, chiamata Merge,
il cui ruolo era quello di combinare in un'unica
lista ordinata gli 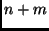 elementi di due liste
(di
elementi di due liste
(di 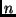 ed
ed 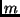 elementi rispettivamente)
ricevute in input.
Il numero di confronti impiegato dalla semplice
procedura che avevamo preso in considerazione era
elementi rispettivamente)
ricevute in input.
Il numero di confronti impiegato dalla semplice
procedura che avevamo preso in considerazione era 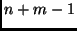 ,
nel caso peggiore.
,
nel caso peggiore.
Domanda 1
Poteva la nostra
Merge impiegare meno di
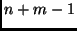
confronti, a seconda delle sequenze ricevute in input?
Domanda 2
Sapresti dire il numero
di confronti impiegato dalla nostra Merge
in media?
Domanda 3
Quale è il minimo numero di confronti che
un qualsiasi algoritmo dovrà impiegare nel suo
caso peggiore per fare il merging di due liste ordinate?
Nel seguito,
assumeremo di ricevere in input due liste ordinate
e
ed assumeremo per semplicità che tutti gli elementi siano distinti.
Indicheremo con 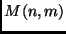 il minimo numero di confronti
che risultino sempre sufficienti alla fusione delle due liste
in inputs in un'unica lista ordinata.
il minimo numero di confronti
che risultino sempre sufficienti alla fusione delle due liste
in inputs in un'unica lista ordinata.
Domanda 4
Sapresti dire perchè sappiamo già
che
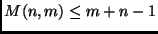
?
Riesci a giustificarti il significato della frase seguente:
``del fatto che
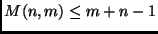
abbiamo già dato
una dimostrazione algoritmica''.
Chiaramente,
gli elementi 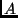 potranno apparire inframmezzati
agli elementi
potranno apparire inframmezzati
agli elementi 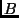 in un totale di
in un totale di
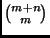 modi diversi.
Pertanto, poichè l'esito di un confronto mi consegna al più
un bit di informazione,
ne consegue che
modi diversi.
Pertanto, poichè l'esito di un confronto mi consegna al più
un bit di informazione,
ne consegue che
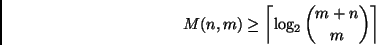 |
(1) |
Esercizio 1
Si noti l'eleganza con cui il lower bound
1
è stato ottenuto sulla base di semplici
considerazioni attinenti alla quantità di informazione,
poggiando sull'ovvio principio che l'informazione
non possa venire dal nulla.
Sapresti formalizzare una nozione di ``quantità
di informazione'' che ti consenta di acquisire
maggiore fiducia nella dimostrazione ora suggerita?
Prova a derivare, in base alla stessa tipologia
di argomenti,
il lower bound di
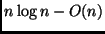
confronti
dato per l'ordinamento.
Esercizio 2
Condurre un'analisi asintotica sul lower bound
1
assumendo che
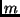
sia costante e facendo crescere
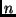
.
Il tuo obbiettivo nel condurre tale analisi
sarà quello di evidenziare quanto esso si discosti
dall'upper bound
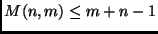
.
Esercizio 3
Se sarai riuscito a portare sufficientemente avanti
l'analisi asintotica di cui all'esercizio
2,
avrai realizzato che il lower bound
1 lascia ampio spazio
al miglioramento della procedura
Merge.
Si mostri come sia in effetti possibile
ridurre il numero di confronti nel caso peggiore quando
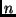
cresce
ed
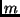
è invece costante.
Ma anche nel caso per noi più significativo,
quando cioè 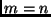 ,
il lower bound proposto non consente
di farci un sandwich con
,
il lower bound proposto non consente
di farci un sandwich con
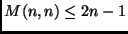 e mostarda,
al fine di argomentare l'ottimalità della nostra procedura Merge.
e mostarda,
al fine di argomentare l'ottimalità della nostra procedura Merge.
Esercizio 4
Partire dalla diseguaglianza
praticamente ricavata qui sopra per giungere
alla formula asintotica
Pertanto,
il lower bound basato
su considerazioni attinenti alla quantità di informazione,
ha il corretto ordine di crescita (ed anche la corretta costante)
ma non consente di dimostrare l'ottimalità
della nostra procedura di Merge.
E tuttavia,
è possibile dimostrare 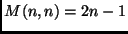 .
.
Teorema 1
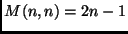
, for
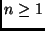
.
Proof:
Si consideri il caso in cui la giusta soluzione
al problema del merging sia costituita da
Ci si chieda:
- sarebbe stato sicuro uscire
dalla procedura senza aver eseguito un confronto del tipo
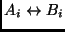 ?
?
- sarebbe stato sicuro uscire
dalla procedura senza aver eseguito un confronto del tipo
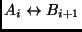 ?
?
Se ne traggano le debite conclusioni.
Per esercizio,
dimostrare ora il seguente teorema,
anch'esso rilevante per le applicazioni di Merge
in seno all'algoritmo MergeSort.
Teorema 2
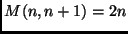
, for
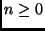
.



Next: About this document ...
Romeo Rizzi
2002-10-07
![]() elementi di due liste
(di
elementi di due liste
(di ![]() ed
ed ![]() elementi rispettivamente)
ricevute in input.
Il numero di confronti impiegato dalla semplice
procedura che avevamo preso in considerazione era
elementi rispettivamente)
ricevute in input.
Il numero di confronti impiegato dalla semplice
procedura che avevamo preso in considerazione era ![]() ,
nel caso peggiore.
,
nel caso peggiore.
![]() potranno apparire inframmezzati
agli elementi
potranno apparire inframmezzati
agli elementi ![]() in un totale di
in un totale di
![]() modi diversi.
Pertanto, poichè l'esito di un confronto mi consegna al più
un bit di informazione,
ne consegue che
modi diversi.
Pertanto, poichè l'esito di un confronto mi consegna al più
un bit di informazione,
ne consegue che
![]() ,
il lower bound proposto non consente
di farci un sandwich con
,
il lower bound proposto non consente
di farci un sandwich con
![]() e mostarda,
al fine di argomentare l'ottimalità della nostra procedura Merge.
e mostarda,
al fine di argomentare l'ottimalità della nostra procedura Merge.
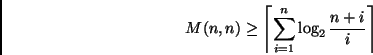
![]() .
.