Algoritmi e Strutture Dati

Il corso ha lo scopo di introdurre le tecniche principali per organizzare in modo efficente i dati e per l'analisi e la progettazione di algoritmi per risolvere problemi complessi. Nel corrispondente corso di laboratorio vengono sperimentate le tecniche studiate a livello teorico nel corso di algoritmi e strutture dati.

Programma del corso:

Analisi degli algoritmi

• Complessità degli algoritmi in tempo e spazio. Nozione di complessità degli algoritmi rispetto al tempo e allo spazio; operazioni caratteristiche.

• Misure di complessità. Complessità asintotica in caso peggiore e in caso medio. Indipendenza della complessità dalla macchina reale.

• Ricorsione e iterazione. Metodi per la valutazione della complessità di algoritmi iterativi e ricorsivi.

• Modelli astratti di Computazione. Cenni ai modelli astratti di macchina e ai metodi di calcolo della complessità relativi.

• Notazioni. Funzioni di confronto; notazione O e $\Theta$.

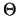Tipi di Dati Astratti

• Livelli di risoluzione dei problemi. Descrizione matematica delle strutture dati e dei metodi risolutivi di un problema. Definizione ad alto livello (metalinguaggio). Codifica di strutture dati e soluzione in un linguaggio di programmazione.

• Concetto di ADT. Tipo di dati astratto ADT come descrizione ad alto livello (con linguaggio matematico) di una struttura dati; insieme degli elementi e operazioni ammesse; operazioni fondamentali, operazioni derivate.

• Codifica di un ADT. Classe come implementazione di un ADT. Invariante di classe. Metodi. Correttezza dell'implementazione.

• Analisi di complessità. Costo computazionale delle operazioni associate ad un ADT. Analisi ammortizzata.

Tecniche di Progettazione degli Algoritmi

• Metodi generali. Algoritmi incrementali del primo e del secondo tipo. Esempi.

• Divide et impera. Descrizione della tecnica ed esempi.

• Programmazione dinamica. Descrizione della tecnica ed esempi.

Tecniche matematiche per l'analisi degli algoritmi

• Notazioni asintotiche.

• Sommatorie. Proprietà fondamentali. Stime di sommatorie.

• Ricorrenze. Metodo di sostituzione. Stime per iterazione. Teorema per la stima delle equazioni di ricorrenza.

Strutture Dati Ricorsive

• Liste, pile e code. Definizione matematica e operazioni notevoli (lunghezza,...); tipo di dati astratto corrispondente; strutture dati concrete. Varianti.

• Alberi n-ari. Definizione matematica e operazioni notevoli (altezza, profondità,...); tipo di dati astratto corrispondente; strutture dati concrete. Alberi n-ari; alberi di ricerca; alberi bilanciati. Alberi di Huffman: scopo, implementazione e correttezza dell'algoritmo di Huffman. Altre varianti.

• Insiemi. Definizione matematica e operazioni notevoli (lunghezza,...); tipo di dati astratto corrispondente; strutture dati concrete. Varianti.

Symbol table

• Specifiche. Definizione matematica e operazioni fondamentali; tipo di dati astratto corrispondente; strutture dati concrete.

• Liste. Implementazione del ADT mediante liste. Valutazione della complessità del ADT. Pregi e difetti dell'implementazione. Euristiche e loro valutazione.

• Alberi di ricerca. Implementazione del ADT mediante alberi di ricerca. Valutazione della complessità del ADT. Pregi e difetti dell'implementazione. Euristiche. Splay trees con analisi ammortizzata.

• B-Trees. Implementazione del ADT mediante B-Trees. Valutazione della complessità del ADT. Pregi e difetti dell'implementazione.

• Hash tables. Implementazione del ADT mediante hash tables; tabelle di dimensione fissa e di dimensione variabile. Altre varianti dell'implementazione. Valutazione della complessità del ADT. Pregi e difetti dell'implementazione.

• Liste con indici. Implementazione del ADT mediante indexed list. Valutazione della complessità del ADT. Pregi e difetti dell'implementazione.

Priority queues

• Specifiche. Definizione matematica e operazioni fondamentali; tipo di dati astratto corrispondente; strutture dati concrete: heap-structure e heap.

• Heap Sort. Descrizione dell'algoritmo; correttezza. Analisi di complessità.

• Altre implementazioni. Implementazione di uno heap come vettore.

Algoritmi di ordinamento

• Descrizione matematica e specifiche del problema.

• Metodi elementari. Ordinamento per selezione e per inserzione. Descrizione degli algoritmi e correttezza. Analisi della complessità.

• MergeSort. Principi di funzionamento. Descrizione dell'algoritmo e correttezza. Analisi della complessità. Varianti.

• QuickSort. Principi di funzionamento. Descrizione dell'algoritmo e correttezza. Analisi della complessità. Varianti.

• RadixSort. Principi di funzionamento. Descrizione dell'algoritmo e correttezza. Analisi della complessità. Varianti.

• Selezione del k-mo elemento minimo. Principi di funzionamento. Descrizione dell'algoritmo e correttezza. Analisi della complessità. Varianti.

Insiemi disgiunti

• Specifiche. Definizione matematica e operazioni fondamentali; tipo di dati astratto corrispondente; possibili strutture dati concrete.

• Rappresentazione di Galler-Fischer. Caratteristiche generali; complessità.

• Unione per dimensione. Analisi di complessità.

• Altre implementazioni possibili.

Grafi

• Introduzione. Definizione matematica di grafo e terminologia; funzioni fondamentali.

• Specifiche. Tipo di dati astratto corrispondente; possibili strutture dati concrete.

• Rappresentazione. Matrice di incidenza, liste di adiacenza.

• Grafi diretti-aciclici. Definizione. Ordinamento topologico.

• Metodi di visita. Visita depth-fist e breadth-first; algoritmo e complessità.

• Algoritmi notevoli. Componenti fortemente connesse: definizione, algoritmo e correttezza. Componenti biconnesse: definizione, algoritmo e correttezza.

Testo adottato: Jeffrey H. Kingston, Algorithms and Data Structures, Addison Wesley Longman, 1998.