Prova Scritta di Programmazione Matematica
- prototipo 1 -
PROBLEMA 1:
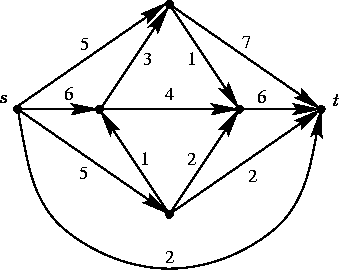
- 1.
- Trovare il flusso massimo da s a t.
- 2.
- Fornire un'argomentazione per l'ottimalità.
- 3.
- Di quali archi posso ridurre la capacità
senza ridurre il valore del flusso massimo?
PROBLEMA 2:
- Risolvere sia per via grafica che algebricamente.
- Se la funzione obiettivo è il profitto di un'attività,
quanto saremmo disposti a pagare per incrementare di un'unità
il termine noto nel primo o secondo vincolo?
E fino a dove saremmo disposti a pagare tale prezzo?
- Di quanto dovremmo alterare ciascun coefficiente nella
funzione obiettivo (singolarmente)
affinchè la soluzione non sia più ottima?
PROBLEMA 3:
- Scrivere il duale e risolverlo per via grafica.
- Utilizzare gli scarti complementari per trovare
la soluzione primale ottima.
PROBLEMA 4:
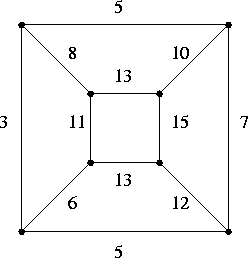
- 1.
- Trovare un accoppiamento perfetto di peso minimo.
- 2.
- Fornire un certificato di ottimalità.
- 3.
- Indicare quali accoppiamenti perfetti
siano ottimi.
PROBLEMA 5(COINCISIONE, CHIAREZZA E SEMPLICITÀ):
- 1.
- Dare una definizione assiomatica di matroide
in base alle proprietà degli insiemi indipendenti.
- 2.
- Dimostrare che le foreste di un grafo formano gli
insiemi indipendenti di un matroide.
- 3.
- Dimostrare che l'algoritmo Greedy ritorna sempre
l'ottimo se la struttura su cui opera è un matroide.
- 4.
- Dare una definizione assiomatica di matroide
utilizzando le proprietà delle basi.
- 5.
- Dimostrare l'equivalenza delle definizioni date.
PROBLEMA 6(FACOLTATIVO):
Dare una dimostrazione di 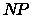 -completezza a scelta.
La meno triviale è, meglio è.
-completezza a scelta.
La meno triviale è, meglio è.
|
Giugno 1998
|
© Dipartimento di Matematica - Università di Trento

|


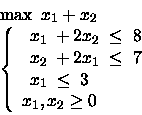
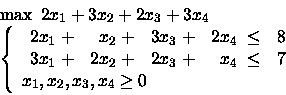

![]() -completezza a scelta.
La meno triviale è, meglio è.
-completezza a scelta.
La meno triviale è, meglio è.
