Provetta sulla PL
PROBLEMA 1:
Considerare la soluzione
x1 = x2 = 3 e
x3 = x4 = 0.
La soluzione proposta è ammissibile?
È di base?
È ottima?
PROBLEMA 2:
Se un problema di PL in forma standard
ha una soluzione ottima non di base allora.

- È necessariamente ammissibile.

- È necessariamente degenere ossia ha
almeno una soluzione di base degenere.

- Può essere illimitato.

- Il duale è necessariamente ammissibile.

- Il duale è necessariamente limitato.

- Ha almeno una soluzione di base ottima.

- Ha almeno due soluzioni di base ottime.
Argomentare sinteticamente ma efficacemente le risposte.
PROBLEMA 3:
Costruire un problema di PL
dove nè il primale nè il duale siano ammissibili.
PROBLEMA 4:
- Risolvere sia per via grafica che algebricamente.
- Se la funzione obiettivo è il profitto di un'attività,
quanto saremmo disposti a pagare per incrementare di un'unità
il termine noto nel primo o secondo vincolo?
E fino a dove saremmo disposti a pagare tale prezzo?
- Di quanto dovremmo alterare ciascun coefficiente nella
funzione obiettivo (singolarmente)
affinchè la soluzione non sia più ottima?
PROBLEMA 5(FACOLTATIVO):
Si cosideri il gioco finito a due giocatori
e somma zero Carta, forbice e sasso.
- Dare la matrice dei pagamenti.
- Dare la strategia mista ottima per il giocatore A e dimostrarne l'ottimalità.
- Mostrare che se A adotta la sua strategia mista ottima
allora nessuna strategia di B risulta preferibile sulle
altre.
- provare o dare un controesempio:
la proprietà discussa al punto precedente
è valida in generale per tutti i giochi finiti
a due giocatori e somma zero.
PROBLEMA 6(FACOLTATIVO):
Dato un sistema di diseguaglianze
dirò che esse implicano
la diseguaglianza
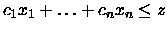 se ogni
se ogni
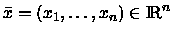 che soddisfa l'insieme
soddisfa anche la diseguaglianza
che soddisfa l'insieme
soddisfa anche la diseguaglianza
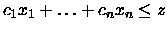 .
Si consideri il problema di decidere se un dato sistema
implichi o meno una data diseguaglianza.
.
Si consideri il problema di decidere se un dato sistema
implichi o meno una data diseguaglianza.
- Impostare come un problema di PL.
- Se l'implicazione vale come posso dimostrarlo succintamente?
Se essa non vale come posso dimostrarlo succintamente?
- Derivarne un teorema che caratterizzi (se e solo se)
quando un insieme di diseguaglianze implichi una diseguaglianza.
In bocca al lupo.
|
23 Aprile 1998
|
© Dipartimento di Matematica - Università di Trento

|
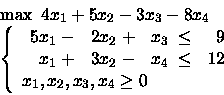
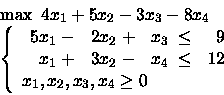
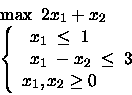
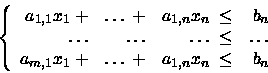
![]() se ogni
se ogni
![]() che soddisfa l'insieme
soddisfa anche la diseguaglianza
che soddisfa l'insieme
soddisfa anche la diseguaglianza
![]() .
Si consideri il problema di decidere se un dato sistema
implichi o meno una data diseguaglianza.
.
Si consideri il problema di decidere se un dato sistema
implichi o meno una data diseguaglianza.
