Svolgimento della Provetta sulla PL

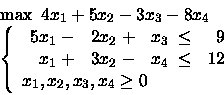
PROBLEMA 1:

$$\begin{array}{l} \max \mbox{\ }4x_1 +5x_2 -3x_3 -8x_4\\ \l... ... x_1, x_2, x_3, x_4 \geq 0 \end{array} \right. \end{array}$$

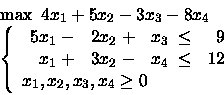
Considerare la soluzione x₁ = x₂ = 3 e x₃ = x₄ = 0. La soluzione proposta è ammissibile? È di base? È ottima?

VERIFICA AMMISSIBILITÀ:

$$\left\{ \begin{array}{l} \begin{array}{rrrrr} 5(3) \;-& 2(... ...\geq 0 \mbox{, \ } x_3 = x_4 = 0 \geq 0 \end{array} \right.$$

la soluzione proposta è ammissibile

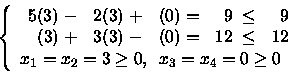
VERIFICO SE È DI BASE:

Devo verificare se x₁, x₂ possano venir espresse in termini delle altre variabili. Computo il seguente determinante:

$$\left\Vert \begin{array}{rr} 5 & -2 \\ 1 & 3 \\ \end{array} \right\Vert = 15 + 2 = 17 \neq 0$$

la soluzione proposta è di base

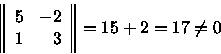
VERIFICA OTTIMALITÀ:

Considero il problema duale:

$$\begin{array}{l} \min \mbox{\ }9y_5 +12y_6\\ \left\{ \beg... ...{array} \\ y_5, y_6 \geq 0 \end{array} \right. \end{array}$$

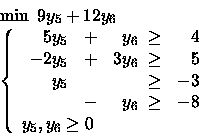
Utilizzo gli scarti complementari:

$$x_1, x_2 > 0 \Longrightarrow \mbox{primo e secondo vincolo soddisfatti ad eguaglianza}$$

Ottengo quindi il sistema:

$$\left\{ \begin{array}{rcrr} 5y_5 &+& y_6 \;= & 4 \\ -2y_5 &+& 3y_6 \;= & 5 \\ \end{array} \\ \right.$$

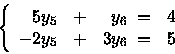
Risolvendo il sistema giungo a proporre la seguente soluzione per il duale:

$$y_5 = \frac{7}{17} \mbox{; \ \ } y_6 = \frac{33}{17}$$

Verifico ora l'ammissibilità di tale soluzione:

$$\left\{ \begin{array}{l} \begin{array}{rcrcrrr} (\frac{7}{... ...0 \mbox{, \ } y_6 = \frac{33}{17} \geq 0 \end{array} \right.$$

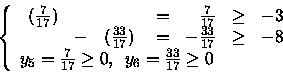
Siccome abbiamo una soluzione primale ammissibile ed una soluzione duale ammissibile che soddisfano gli scarti complementari posso di già concludere per l'ottimalità di tali soluzioni.

In effetti i valori delle funzioni obiettivo in corrispondenza di tali soluzioni coincidono.

$$z = 4(3) +5(3) -3(0) -8(0) = {\bf 27} = 9(\frac{7}{17}) +12(\frac{33}{17}) = w$$

la soluzione proposta è ottima ed un certificato di ottimalità è il seguente:

$$z = 4x_1 +5x_2 -3x_3 -8x_4 \leq \frac{7}{17} (5x_1 -2x_2 +x... ... +3x_2 -x_4) \leq \frac{7}{17} (9) + \frac{33}{17} (12) = 27$$

PROBLEMA 2: Se un problema di PL in forma standard ha una soluzione ottima non di base allora.

$\Box$

È necessariamente ammissibile. VERO

$\Box$

È necessariamente degenere ossia ha almeno una soluzione di base degenere. FALSO

$\Box$

Può essere illimitato. FALSO

$\Box$

Il duale è necessariamente ammissibile. VERO

$\Box$

Il duale è necessariamente limitato. VERO

$\Box$

Ha almeno una soluzione di base ottima. VERO

$\Box$

Ha almeno due soluzioni di base ottime. FALSO

Argomentiamo ora le risposte.

Per la dualità, quando un problema di PL ha una soluzione ottima anche il suo duale ha una soluzione ottima e di pari valore. Quindi primale e duale sono entrambi ammissibili e limitati.

Il teorema fondamentale della PL stabilisce che quando un problema in forma standard ha una soluzione ottima allora esso ha almeno una soluzione ottima di base. Mostrare con un esempio come tale implicazione non sia più vera qualora il problema non sia in forma standard.

Se la regione ammissibile fosse poi limitata potremmo trarne le seguenti conseguenze:

In questo caso poi di soluzioni ottime di base devono essercene almeno due. Infatti se x è la mia soluzione ottima non di base essa sarà esprimibile come combinazione convessa di almeno due soluzioni di base. Siccome x è ottima allora tutte le soluzioni di base utilizzate nella combinazione convessa saranno ottime.

Si consideri ora il dizionario associato ad una qualsiasi soluzione di base ottima. La funzione obiettivo non cambia valore nel passare da tale soluzione di base a qualsiasi altra soluzione di base ottima. Questo dizionario è pertanto degenere.

Tali conclusioni cessano tuttavia di valere se la regione ammissibile non è limitata. Ciò è posto in evidenza dal seguente problema in forma standard.

$$\begin{array}{l} \max \; \; x_2\\ \left\{ \begin{array}{l... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

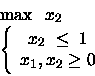
Esso presenta un'unica soluzione di base (e non degenere) nonostante ammetta soluzioni ottime non di base.

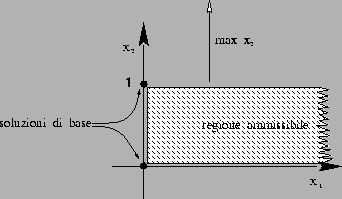
PROBLEMA 3: Costruire un problema di PL dove nè il primale nè il duale siano ammissibili.

Si consideri il seguente problema di PL

$$\begin{array}{l} \max \mbox{\ }x_1 +x_2\\ \left\{ \begin{... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

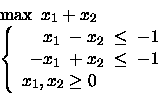
La seconda diseguaglianza può essere riscritta come $x_1 - x_2 \geq 1$ed è quindi in contraddizione con la prima diseguaglianza. Il problema è pertanto inammissibile.

Il duale contiene le seguenti due diseguaglianze $-y_3 + y_4 \geq 1$ e $y_3 - y_4 \geq 1$ che sono di nuovo in contraddizione. Il problema duale è pertanto inammissibile.

Il problema proposto ha la seguente proprietà: la descrizione del problema duale (come ottenuta seguendo il procedimento standard) è equivalente alla descrizione del problema primale. Sapresti caratterizzare per quali problemi di PL vale tale proprità, eventualmente restringendoti a considerare problemi con vettore dei coefficienti della funzione obiettivo c=1e vettore dei termini noti b=-1?
Tra questi problemi, quali sono quelli ammissibili?

PROBLEMA 4:

$$\begin{array}{l} \max \mbox{\ }2x_1 +x_2\\ \left\{ \begin... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

• Risolvere sia per via grafica che algebricamente.
• Se la funzione obiettivo è il profitto di un'attività, quanto saremmo disposti a pagare per incrementare di un'unità il termine noto nel primo o secondo vincolo? E fino a dove saremmo disposti a pagare tale prezzo?
• Di quanto dovremmo alterare ciascun coefficiente nella funzione obiettivo (singolarmente) affinchè la soluzione non sia più ottima?

RISOLUZIONE GRAFICA:

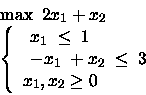
Rappresentiamo in figura lo spazio delle soluzioni ammissibili, il gradiente della funzione obiettivo e la soluzione ottima.

 

Figure 1: regione ammissibile e soluzione ottima.

RISOLUZIONE ALGEBRICA:

Il problema è in forma canonica e pertanto gli corrisponde il primo dei seguenti tre tableau. Il problema è ad origine ammissibile e pertanto impiego il metodo del simplesso primale per giungere al tableau ottimo.

$$\begin{array}{rrrr} & x_1 & x_2 \\ x_3 & \fbox{$1$ } & 0 &... ... 0 & 1 \\ x_2 & 1 & 1 & 4 \\ z & 3 & 1 & 6 \\ \end{array}$$

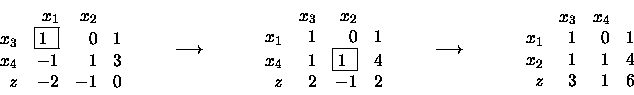
Pertanto la soluzione ottima è x₁ = 1, x₂ = 4. Ad essa corrisponde un valore di 6della funzione obiettivo.

I valori delle variabili duali (prezzi ombra) sono y₃ = 3, y₄ = 1. Pertanto:

• per ogni unità di incremento nel termine noto del primo vincolo sono disposto a pagare al massimo 3.
• per ogni unità di incremento nel termine noto del secondo vincolo sono disposto a pagare al massimo 4.

Tuttavia questa indicazione vale solo per piccoli incrementi. Per scoprire fino a quali entità di incremento tali valori restano validi passiamo a considerare il duale. Il tableau del duale all'ottimo può essere ottenuto dal tableau primale all'ottimo come segue:

$$\begin{array}{c} \mbox{\sc Tableau Primale}\\ \begin{array... ... & 0 & -1 & 1 \\ z & -1 & -4 & 6 \\ \end{array} \end{array}$$

Assumiamo di incrementare di D la disponibilità nel primo vincolo. Il vantaggio nel considerare il duale é che l'unica riga ad essere influenzata da questa modifica nel problema è l'ultima. La nuova riga può essere prodotta attraverso opportune sostituzioni o avvalendosi della PROVA DI CONTROLLO (prova del nove) della PL.

$$\begin{array}{rrrrr} & & (0) & (0) \\ & & \downarrow \;& \... ...rrow & y_4 & 0 & -1 & 1 \\ & z & -1 & -4 & 6 \\ \end{array}$$

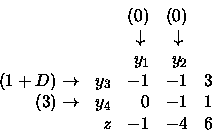
Ricordiamo che per ogni colonna vale quanto segue: il valore dell'ultimo elemento della colonna si ottiene sommando gli altri elementi della colonna ciascuno moltiplicato per il coefficiente della riga cui appartiene e sottraendo infine il valore del coefficiente associato alla colonna.

Colonna 1: -1(1+D)+0(3)-(0)= -1 -D
Colonna 2: -1(1+D)-1(3)-(0)= -4 -D
Colonna 3: 3(1+D)+1(3) = 6+3D

Pertanto la riga prodotta è:

$$\begin{array}{lll} -(1+D) & -(4+D) & (6+3D) \\ \end{array}$$

Siccome il tableau resta ottimo per ogni $D\geq -1$concludo che non vi sono limitazioni nel quantitativo di diponibilità del primo vincolo che siamo disposti ad acquistare pagando 3 per ogni unità di incremento.

Consideriamo ora il secondo vincolo:

$$\begin{array}{rrrrr} & & (0) & (0) \\ & & \downarrow \;& \... ...rrow & y_4 & 0 & -1 & 1 \\ & z & -1 & -4 & 6 \\ \end{array}$$

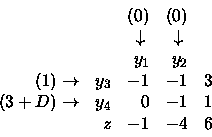
Colonna 1: -1(1)+0(3+D)-(0)= -1
Colonna 2: -1(1)-1(3+D)-(0)= -4 -D
Colonna 3: 3(1)+1(3+D) = 6+D

Pertanto la riga prodotta è:

$$\begin{array}{lll} -1 & -(4+D) & (6+D) \\ \end{array}$$

Siccome il tableau resta ottimo per ogni $D\geq -4$concludo che non vi sono limitazioni nel quantitativo di diponibilità del secondo vincolo che siamo disposti ad acquistare pagando 4 per ogni unità di incremento.

Nel analizzare la sensitività della soluzione ottima rispetto a modifiche dei coefficienti della funzine obiettivo conviene invece riferirsi al primale.

$$\begin{array}{rrrrr} & & (0) & (0) \\ & & \downarrow \;& \... ...htarrow & x_2 & 1 & 1 & 4 \\ & z & 3 & 1 & 6 \\ \end{array}$$

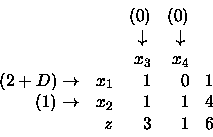
Utilizzo nuovamente la regola di controllo

Colonna 1: 1(2+D)+1(1)-(0)= 3+D
Colonna 2: 0(2+D)+1(1)-(0)= 1
Colonna 3: 1(2+D)+4(1) = 6+D

Pertanto la riga prodotta è:

$$\begin{array}{lll} (3+D) & 1 & (6+D) \\ \end{array}$$

Siccome il tableau resta ottimo per ogni $D\geq -3$concludo che la soluzione proposta (x₁ = 1, x₂ = 4.) resta ottima fintantochè $D\geq -3$.

Consideriamo ora il secondo coefficiente della funzione obiettivo.

$$\begin{array}{rrrrr} & & (0) & (0) \\ & & \downarrow \;& \... ...htarrow & x_2 & 1 & 1 & 4 \\ & z & 3 & 1 & 6 \\ \end{array}$$

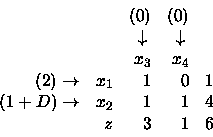
Utilizzo nuovamente la regola di controllo

Colonna 1: 1(2)+1(1+D)-(0)= 3+D
Colonna 2: 0(2)+1(1+D)-(0)= 1+D
Colonna 3: 1(2)+4(1+D) = 6+4D

Pertanto la riga prodotta è:

$$\begin{array}{lll} (3+D) & (1+D) & (6+4D) \\ \end{array}$$

Siccome il tableau resta ottimo per ogni $D\geq -1$concludo che la soluzione proposta (x₁ = 1, x₂ = 4.) resta ottima fintantochè $D\geq -1$.

Risulta a questo punto istruttivo rappresentare le due funzioni obiettivo estremali ( z=-x₁+x₂ e z=2x₁) nel piano cartesiano. L'analisi di sensitività poteva anch'essa essere condotta per via geometrica. Come esercizio aggiuntivo propongo di analizzare modifiche congiunte nei due coefficienti ossia:

$$\begin{array}{rrrrr} & & (0) & (0) \\ & & \downarrow \;& \... ...htarrow & x_2 & 1 & 1 & 4 \\ & z & 3 & 1 & 6 \\ \end{array}$$

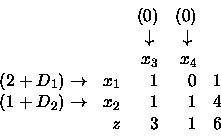
PROBLEMA 5(FACOLTATIVO): Si cosideri il gioco finito a due giocatori e somma zero Carta, forbice e sasso.

• Dare la matrice dei pagamenti.
• Dare la strategia mista ottima per il giocatore A e dimostrarne l'ottimalità.
• Mostrare che se A adotta la sua strategia mista ottima allora nessuna strategia di B risulta preferibile sulle altre.
• provare o dare un controesempio: la proprietà discussa al punto precedente è valida in generale per tutti i giochi finiti a due giocatori e somma zero.

MATRICE DEI PAGAMENTI:

	C	F	S
C	0	-1	1
F	1	0	-1
S	-1	1	0

	[C] Carta
	[F] Forbice
	[S] Sasso

STRATEGIA MISTA OTTIMA:

Si consideri la strategia mista $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. Valutiamo l'aspettazione di vincita di tale strategia contro le tre strategie pure di B:

Carta

$E[vincita/C] = \frac{1}{3}(0)+\frac{1}{3}(-1)+\frac{1}{3}(1) =0$

Forbice

$E[vincita/F] = \frac{1}{3}(1)+\frac{1}{3}(0)+\frac{1}{3}(-1) =0$

Sasso

$E[vincita/S] = \frac{1}{3}(-1)+\frac{1}{3}(1)+\frac{1}{3}(0) =0$

Nel caso peggiore un'aspettazione di vincita pari a 0è garantita per la strategia mista $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. Ossia $0=\min\{E[vincita/C],\; E[vincita/F],\;E[vincita/S]\}$ è il valore da attribuire alla strategia $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$. Siccome la matrice dei pagamenti è antisimmetrica (i ruoli dei due giocatori sono analoghi ed interscambiabili) il gioco è equo ossia di valore 0. Pertanto la strategia proposta è ottima.

Era possibile giungere alla stessa conclusione fornendo una strategia di valore 0anche per il giocatore B. Poichè il valore di ogni strategia di A è minore o eguale a quello di ogni strategia di B ne sarebbe derivata l'ottimalità di entrambe le strategie. Potresti fornire una strategia di valore 0per il giocatore B? Tale strategia è unica? Perchè?

CONSIDERAZIONI SULLA STRATEGIA DI B A GIOCO OTTIMO DI A:

Torniamo a considerare l'aspettazione di vincita della strategia $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ per A contro le tre strategie pure di B. Su ciascuna di tali strategie abbiamo ottenuto il valore 0. Poichè ogni strategia mista di B è combinazione convessa di strategie pure di B la stessa conclusione deve valere per ogni strategia (pura o mista) di B. Pertanto, se fosse garantito che A si attiene alla strategia ottima, la scelta sulla strategia di B risulterebbe ininfluente agli effetti del gioco.

CONTROESEMPIO:

Si consideri la seguente matrice di pagamenti:

	Strategia 1	Strategia 2
Unica Strategia	-1	1

Oppure si estenda il gioco Carta, forbice e sasso come segue:

	C	F	S	Suicidio
C	0	-1	1	100
F	1	0	-1	100
S	-1	1	0	100

Si osservi che entrambi sono giochi finiti a due giocatori e somma zero. Il secondo di essi è inoltre un gioco equo. (La definizione di equità non contempla le maggiori possibilità che B ha di sbagliare). Tuttavia nessuno dei due giochi è simmetrico (ossia le matrici dei pagamenti non sono antisimmetriche). Sapresti ora costruire un controesempio simmetrico?

Una seconda caratteristica dei controesempi forniti è che essi contemplano per il giocatore B una strategia dominata da qualche altra strategia, ossia una colonna della matrice dei pagamenti domina (maggiore o eguale su ogni singola componente) una qualche altra colonna. Il giocatore B dovrebbe essere un suicida per utilizzare la strategia corrispondente ad una tale colonna. Sapresti fornire un controesempio dove tale dominanza non sia presente?

Vista infine l'abbondanza di controesempi ottenuti, sapresti caratterizzare quali siano i giochi che non sono controesempi?

PROBLEMA 6(FACOLTATIVO): Dato un sistema di diseguaglianze

$$\left\{ \begin{array}{rrrr} a_{1,1}x_1 \;+& \ldots \;+& a_{... ...& \ldots \;+& a_{1,n}x_n \;\leq & b_n \\ \end{array} \right.$$

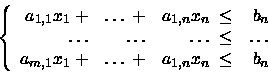
dirò che esse implicano la diseguaglianza $c_1x_1 + \ldots + c_n x_n \leq z$se ogni $\bar{x}=(x_1,\ldots, x_n)\in {\rm I\!R}^n$che soddisfa l'insieme soddisfa anche la diseguaglianza $c_1x_1 + \ldots + c_n x_n \leq z$. Si consideri il problema di decidere se un dato sistema implichi o meno una data diseguaglianza.

• Impostare come un problema di PL.
• Se l'implicazione vale come posso dimostrarlo succintamente? Se essa non vale come posso dimostrarlo succintamente?
• Derivarne un teorema che caratterizzi (se e solo se) quando un insieme di diseguaglianze implichi una diseguaglianza.

Si consideri il seguente problema di PL:

$$\begin{array}{l} \max \mbox{\ }c_1x_1 + \ldots + c_n x_n\\ ... ...& a_{1,n}x_n \;\leq & b_m \\ \end{array} \right. \end{array}$$

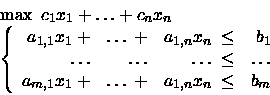
Se il problema è inammissibile allora il sistema, non ammettendo alcuna soluzione, implica banalmente la diseguaglianza. Se il problema è illimitato allora il sistema non implica la diseguaglianza dacchè il sistema ammette soluzioni con $c_1x_1 + \ldots + c_n x_n$ arbitrariamente grande.

Altrimenti siano $\bar{x}_1, \ldots, \bar{x}_n$e $\bar{y}_1, \ldots, \bar{y}_m$una soluzione primale ed una soluzione duale ottima. Sia V il valore della funzione obiettivo.

Se V > z allora l'implicazione non vale e posso argomentare tale conclusione fornendo la soluzione primale $\bar{x}_1, \ldots, \bar{x}_n$. Essa soddisfa al sistema e tuttavia $c_1\bar{x}_1, \ldots, c_n\bar{x}_n = V > z$.

Se $V \leq z$ allora l'implicazione vale e posso argomentare tale conclusione fornendo la soluzione duale $\bar{y}_1, \ldots, \bar{y}_m$. Infatti per ogni soluzione $x_1, \ldots, x_n$del sistema avremo che

$$\sum_{j=1}^n c_j x_j = \sum_{j=1}^n \left(\sum_{i=1}^m \bar{... ... x_j\right) \bar{y}_i = \sum_{i=1}^m b_i \bar{y}_i = V \leq z$$

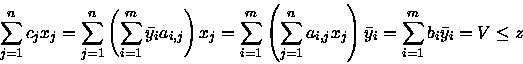
Dal teorema della dualità possiamo pertanto derivare una buona caratterizzazione di quando un sitema di diseguaglianze implichi o meno un'ulteriore diseguaglianza. Siano $a_1, \ldots, a_m \in {\rm I\!R}_n$ i vettori dei coefficienti delle incognite nelle diseguaglianze costituenti il sistema. Sia c il vettore dei coefficienti delle incognite nella diseguaglianza aggiuntiva.

Teorema 1   Il sistema di diseguaglianze $Ax\leq b$ implica la diseguaglianza $cx\leq z$ se e solo se esite una scrittura di c come combinazione lineare $\sum_{i=1}^m \lambda_i a_i$ degli a_i con $\sum_{i=1}^m \lambda_i b_i \leq z$.