Correzione Compito del 29 Ottobre 1998 - Programmazione Matematica

Programmazione Matematica
Correzione Compito del 29 Ottobre 1998

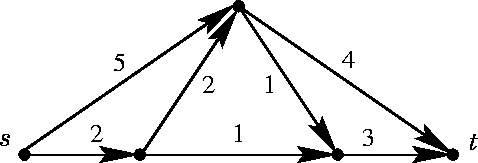
PROBLEMA 1:

$\begin{figure}% \begin{center} \leavevmode \psfig{figure=digraph.eps, height=3.6 true cm}\par\end{center}\end{figure}$

1.: Fornire un flusso massimo da s a t.
2.: Fornire un'argomentazione per l'ottimalità.
3.: Di quali archi posso ridurre la capacità senza ridurre il valore del flusso massimo?
4.: Formulare come un problema di PL dove le variabili di decisione definiscano una circolazione.
5.: Scrivere il duale.
6.: Fornire una soluzione primale ottima ed una soluzione duale ottima.

Flusso e taglio ottimo sono riportati in figura:

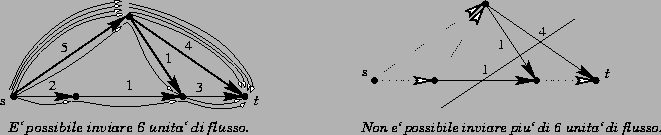
$\begin{figure}% \begin{center} \leavevmode \hfill \psfig{figure=flow.eps, hei... ...\hfill \psfig{figure=cut.eps, height=3 true cm} \hfill \end{center}\end{figure}$

Introduco le variabili di decisione ed etichetto i nodi come suggerito in figura:
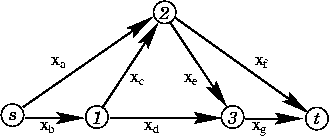
$\begin{figure}% \begin{center} \leavevmode \psfig{figure=etichette.eps, height=3 true cm}\par\end{center}\end{figure}$

La circolazione di valore massimo può essere reperita risolvendo il seguente problema di PL.

Question 1 Sapresti spiegare come la circolazione di valore massimo possa essere reperita risolvendo il seguente problema di PL? Sapresti spiegarne il perchè?

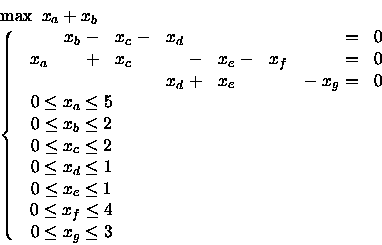
$\begin{displaymath}\begin{array}{l} \max \mbox{\ }x_a +x_b\\ \left\{ \begin{... ...eq x_g \leq 3 \\ \end{array} \end{array} \right. \end{array}\end{displaymath}$

Scrivo il problema duale. Avrò delle variabili duali di nodo ( $\lambda_1,\lambda_2$ e $\lambda_3$ ) e delle variabili duali di arco ( $\lambda_a,\lambda_b,\lambda_c,\lambda_d,\lambda_e,\lambda_f$ e $\lambda_g$ ). Queste ultime dovranno essere non-negative.

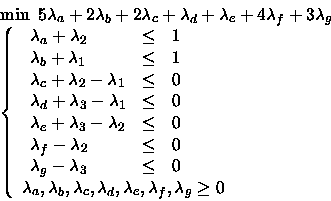
$\begin{displaymath}\begin{array}{l} \min \mbox{\ }5\lambda_a +2\lambda_b +2\lam... ...e,\lambda_f,\lambda_g \geq 0 \end{array} \right. \end{array}\end{displaymath}$

Riesci ad estrapolare la struttura del problema duale per un generico problema primale di circolazione massima in un digrafo capacitato?

Si osservi che

x_a=5, x_b=1, x_c=0, x_d=1, x_e=1, x_f=4, x_g=2

per il primale, e

$\begin{displaymath}\lambda_1=1, \lambda_2=1, \lambda_3=0, \lambda_a=0, \lambda_b... ...lambda_c=0, \lambda_d=1, \lambda_e=1, \lambda_f=1, \lambda_g=0 \end{displaymath}$

per il duale, sono soluzioni ammissibili. Entrambe le soluzioni danno 6 come valore della rispettiva funzione obiettivo. Entrambe le soluzioni sono pertanto ottime. (Perchè?)

Question 2 Che relazione sussiste tra la soluzione primale ed un massimo flusso?
Che relazione sussiste tra la soluzione duale ed un minimo taglio?

Question 3 Utilizzando gli scarti complementari ti sarebbe possibile ricostruire la soluzione duale ottima a partire da quella primale? E viceversa? Sai dartene una motivazione?

PROBLEMA 2:

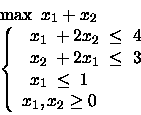
$\begin{displaymath}\begin{array}{l} \max \mbox{\ }x_1 +x_2\\ \left\{ \begin{... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}\end{displaymath}$

1.: Risolvere sia per via grafica che algebricamente.
2.: Se la funzione obiettivo è il profitto di un'attività, quanto saremmo disposti a pagare per incrementare di un'unità il termine noto nel primo o secondo vincolo? E fino a dove saremmo disposti a pagare tale prezzo?
3.: Di quanto dovremmo alterare ciascun coefficiente nella funzione obiettivo (singolarmente) affinchè la soluzione non sia più ottima?

PROBLEMA 3:

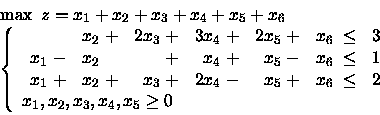
$\begin{displaymath}\begin{array}{l} \max \mbox{\ }z = x_1 +x_2 +x_3 + x_4 +x_5 ... ...1, x_2, x_3, x_4, x_5 \geq 0 \end{array} \right. \end{array}\end{displaymath}$

Si consideri la soluzione: $x_1=\frac{3}{2}, \; x_2=\frac{2}{3}, \; x_5=\frac{5}{6}, \; x_6=\frac{2}{3}, \; x_3 = x_4 = 0$ .

1.: È ammissibile?
2.: È ottima?
3.: È di base?
4.: Trovare le soluzioni ottime di base. (Avvalersi del lavoro svolto al punto 2.).

VERIFICA AMMISSIBILITÀ:

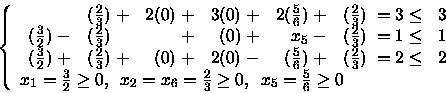
$\begin{displaymath}\left\{ \begin{array}{l} \begin{array}{rrrrrrr} & (\frac{2... ...0 \mbox{, \ } x_5 = \frac{5}{6} \geq 0 \end{array} \right. \end{displaymath}$

la soluzione proposta è ammissibile

VERIFICO SE È DI BASE:

la soluzione proposta non può essere di base poichè presenta 4 variabili di decisione non nulle contro 3 soli vincoli nella formulazione primale assegnata.

VERIFICA OTTIMALITÀ:

Considero il problema duale:

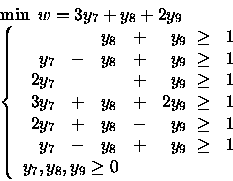
$\begin{displaymath}\begin{array}{l} \min \mbox{\ }w = 3y_7 +y_8 +2y_9\\ \left... ...y} \\ y_7, y_8, y_9 \geq 0 \end{array} \right. \end{array}\end{displaymath}$

Utilizzo gli scarti complementari:

$\begin{displaymath}x_1, x_2, x_5, x_6 > 0 \Longrightarrow \mbox{I$^o$ , II$^o$ ,... ... e VI$^o$\space vincolo del duale soddisfatto ad eguaglianza} \end{displaymath}$

Ottengo quindi il sistema:

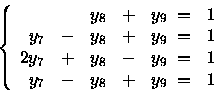
$\begin{displaymath}\left\{ \begin{array}{rcrcrr} & & y_8 &+& y_9 \;= & 1 \\ ... ...\\ y_7 &-& y_8 &+& y_9 \;= & 1 \\ \end{array} \\ \right. \end{displaymath}$

Risolvendo il sistema giungo a proporre la seguente soluzione per il duale:

$\begin{displaymath}y_7 = \frac{1}{3} \mbox{; \ \ } y_8 = \frac{1}{6} \mbox{; \ \ } y_9 = \frac{5}{6} \end{displaymath}$

Verifico ora l'ammissibilità di tale soluzione:

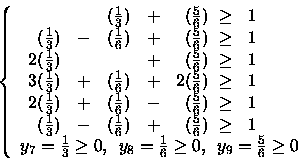
$\begin{displaymath}\left\{ \begin{array}{l} \begin{array}{rcrcrr} & & (\frac{... ... 0 \mbox{, \ } y_9 = \frac{5}{6} \geq 0 \end{array} \right. \end{displaymath}$

Siccome abbiamo una soluzione primale ammissibile ed una soluzione duale ammissibile che soddisfano gli scarti complementari posso di già concludere per l'ottimalità di tali soluzioni.

In effetti i valori delle funzioni obiettivo in corrispondenza di tali soluzioni coincidono.

$\begin{displaymath}z = \left(\frac{3}{2}\right) +\left(\frac{2}{3}\right) +(0) +... ...ght) +\left(\frac{1}{6}\right) +2\left(\frac{5}{6}\right) = w \end{displaymath}$

la soluzione proposta è ottima ed un certificato di ottimalità è costituito dalla soluzione duale da noi reperita attraverso le condizioni degli scarti complementari.

TROVO LE SOLUZIONI OTTIME DI BASE:

Nel fare questo mi avvarrò del certificato di ottimalità. Più precisamente la soluzione duale ottima sopra reperita caratterizzerà (tramite gli scarti complementari) l'insieme di tutte le soluzioni ottime.

Utilizzo gli scarti complementari:

$\begin{displaymath}y_7, y_8, y_9 > 0 \Longrightarrow \mbox{I$^o$ , II$^o$\spac... ...III$^o$\space vincolo del primale soddisfatto ad eguaglianza} \end{displaymath}$

Inoltre:

$\begin{displaymath}\mbox{III$^o$\space e IV$^o$\space vincolo del duale soddisfatto a diseguaglianza} \Longrightarrow x_3, x_4 = 0 \end{displaymath}$

L'insieme delle soluzioni ottime è pertanto il seguente:

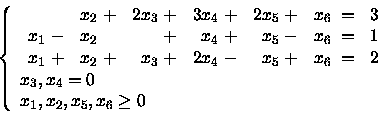
$\begin{displaymath}\left\{ \begin{array}{l} \begin{array}{rrrrrrr} & x_2 \;+&... ..._3, x_4 = 0\\ x_1, x_2, x_5, x_6 \geq 0 \end{array} \right. \end{displaymath}$

Eliminiamo la x₃ e la x₄ che sono nulle. Osserviamo inoltre che sommando la seconda e la terza equazione otteniamo $x_1 = \frac{3}{2}$ . Una formulazione più compatta per l'insieme delle soluzioni ottime è pertanto la seguente:

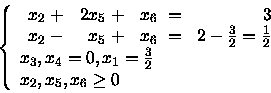
$\begin{displaymath}\left\{ \begin{array}{l} \begin{array}{rrrr} x_2 \;+& 2x_5... ..._1 = \frac{3}{2}\\ x_2, x_5, x_6 \geq 0 \end{array} \right. \end{displaymath}$

Il numero delle possibili basi sarà pertanto ${{3}\choose{2}}=3$ ossia in quanti modi posso scegliere le due variabili da metere in base tra x₂, x₅ ed x₆.

Le tre soluzioni ottime di base sono:

$\begin{displaymath}\begin{array}{l} x_1 = \frac{3}{2}, x_2 = x_3, x_4 = 0, x... ...x_2 = \frac{4}{3} \mbox{\hspace{2cm} Ammissibile!} \end{array}\end{displaymath}$

Di fatto avrei potuto arrivare direttamente alla stessa conclusione osservando come nel problema originario le variabili x₂ ed x₆ svolgessero ovunque il medesimo ruolo.

PROBLEMA 4:

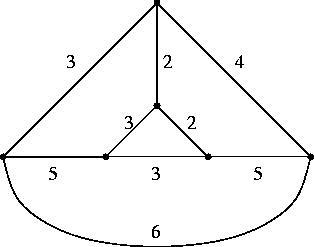
$\begin{figure}% \begin{center} \leavevmode \psfig{figure=oddTetra.eps, height=5.5 true cm}\par\end{center}\end{figure}$

1.: Fornire un accoppiamento perfetto di peso minimo.
2.: Fornire un certificato di ottimalità.
3.: Indicare quali accoppiamenti perfetti siano ottimi, motivando la risposta con riferimento al certificato di ottimalità fornito al punto 2.).

Gli accoppiamenti ottimi sono i seguenti.
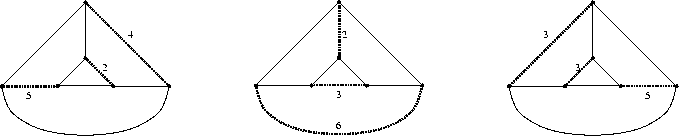
$\begin{figure}% \begin{center} \leavevmode \hfill \psfig{figure=ott1.eps, hei... ...hfill \psfig{figure=ott3.eps, height=3 true cm} \hfill \end{center}\end{figure}$

Il certificato di ottimalità è il seguente:

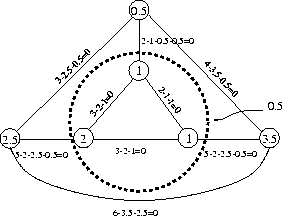
$\begin{figure}% \begin{center} \leavevmode \psfig{figure=prova.eps, height=4.8 true cm}\par\end{center}\end{figure}$

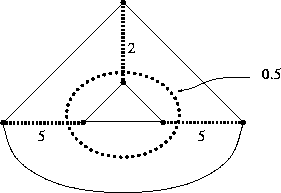
Siccome il costo ridotto di ogni arco è zero tutti gli accoppiamenti perfetti, eccetto quelli che intersecano la componente dispari associata alla variabile duale di valore 0.5, sono ottimi. In pratica l'unico accoppiamento non ottimo è il seguente (interseca 3 volte tale componente dispari):

$\begin{figure}% \begin{center} \leavevmode \psfig{figure=cattivo.eps, height=4.3 true cm}\par\end{center}\end{figure}$

PROBLEMA 5(COINCISIONE, CHIAREZZA E SEMPLICITÀ):

1.: Dimostrare la formula di Eulero per grafi planari
2.: Utilizzare la formula di Eulero per dimostrare che K₅ e K_3,3 non sono planari.

Data una rappresentazione piana di un grafo G, sia n il numero dei nodi, m il numero degli archi ed f il numero delle facce. (In principio potrebbero esistere grafi in cui fdipende dalla particolare rappresentazione piana scelta). Qualora G sia connesso, la formula di Eulero recita: f=m-n+2. Sia T un albero ricoprente di G. Qualora G sia aciclico (ossia G=T) abbiamo m=n-1 e poichè f=1 la formula risulta verificata. Altrimenti G contiene un arco non in Tossia è stato ottenuto da un altro grafo connesso aggiungendo un arco. Tuttavia l'aggiunta di un arco non altera ned incrementa m ed f entrambi di 1.

Exercise 1 Generalizzare la formula di Eulero al caso di k componenti connesse.

Question 4 Esistono davvero grafi planari per cui f dipende dalla particolare rappresentazione piana scelta? Perchè?

Indichimao con K₅^*il duale di K₅ossia quel grafo planare ottenuto da una rappresentazione piana di K₅ponendo un nodo al centro di ogni faccia e congiungendo (con archi) i nodi relativi a faccie confinanti. In pratica K₅ e K₅^*avranno lo stesso numero di archi.

K₅^* dovrebbe avere f=10-5+2=7nodi. Siccome K₅ è semplice (nè autoanelli nè archi paralleli), ogni nodo di K₅^*ha grado almeno 3. Ma allora K₅^* ha almeno $\lceil \frac{3*7}{2} \rceil = \lceil \frac{21}{2} \rceil = 11$ archi. Contraddizione!

Exercise 2 Dimostrare che K_3,3 è non planare. Sugg: Occorre avvalersi del fatto che K_3,3 non solo è semplice ma anche bipartito (e quindi senza triangoli).

29 ottobre 1998