Flusso massimo e cammini aumentanti

Esempi patologici

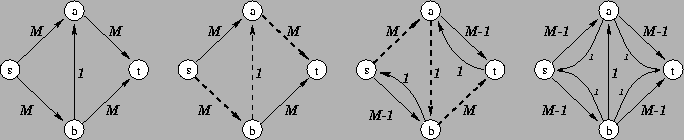
Nel caso di capacità intere (o razionali) il numero di iterazioni (numero di cammini aumentanti impiegati) per raggiungere l'ottimo dipende in generale dai valori delle capacità. Pertanto l'algoritmo che ne deriva non è polinomiale ma solamente pseudopolinomiale dato che la ``magnitudo'' di un valore numerico cresce esponenzialmente nel numero di bit impiegati nel rappresentarlo. Ecco un esempio di tale comportamento:

Supponiamo poi che i possibili valori di capacità siano gli interi più un ulteriore simbolo, $\infty$, rappresentante un valore di capacità infinito, ossia nessun limite all'utilizzo di un dato arco.

Esercizio 1   Modificare l'esempio dato sopra per ottenere un problema dove il valore del flusso sia $\infty$, ossia non limitato, ed una scelta infelice di cammini ad ogni iterazione porti l'algoritmo a non terminare.

Esercizio 2   Proporre una semplice modifica all'algoritmo che consenta di evitare il problema di cui all'esercizio precedente.

Qualora le capacità fossero numeri reali, allora l'algoritmo potrebbe non terminare anche su problemi a valore di flusso massimo limitato. Ciò è posto in evidenza dall'esempio seguente, dove abbiamo deciso di accettare cammini aumentanti che passino piú volte per uno stesso nodo (percorrendo però ogni arco al più una volta).

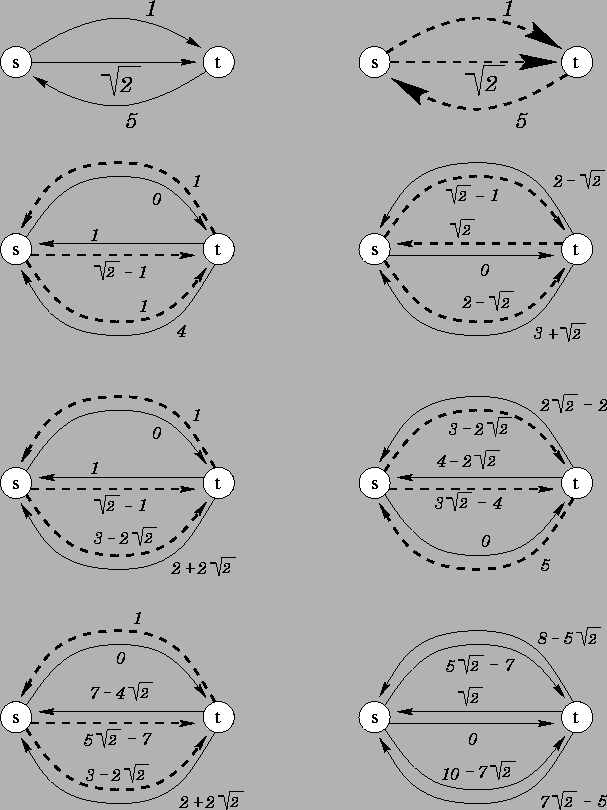
Osserviamo come in questo caso il valore del flusso computato converga verso il valore ottimo.

Esercizio 3   Modificare l'esempio proposto per ottenere un problema dove il valore del flusso computato non converga al valore ottimo.

Se la nostra definizione di cammini aumentanti non vi convince appieno vi consigliamo il seguente esercizio.

Esercizio 4   Modificare gli esempi considerati in modo da ottenere esempi in cui i cammini aumentanti considerati siano cammini semplici (senza ripetizione di nodi).