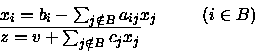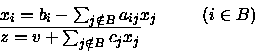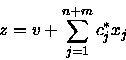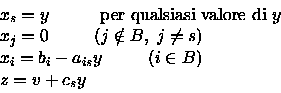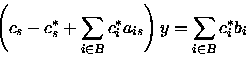Homeworks proposti in data 10 Marzo 1998
Contenuto della lezione del 10 Marzo 1998
Nel 1977 R. G. Bland propose la regola
dell'indice minimo per impedire al metodo
del simplesso di ciclare.
REGOLA DELL'INDICE MINIMO:
si consideri di aver introdotto un ordinamento
totale sugli indici delle variabili.
Quando più variabili si presentano come candidate
per entrare in base (costo ridotto positivo)
allora scelgo la variabile di indice inferiore.
Quando più variabili (degenerazione) si presentano come candidate
per uscire di base (valore nullo nella soluzione associata
al prossimo dizionario o tableau)
allora scelgo la variabile di indice inferiore.
Si noti come la regola di Bland,
a differenza dei metodi antidegenerativi quali
il metodo lessicografico e quello delle perturbazioni,
determini non solo la variabile uscente
ma anche la variabile che entra in base.
Effettivamente questo inconveniente inibì (almeno in un primo momento)
la sua adozione.
Abbiamo dedicato buona parte della
lezione alla dimostrazione del seguente risultato:
Teorema 1 (R. G. Bland 1977)
Qualora la regola dell'indice minimo
venga adottata,
allora il metodo del simplesso
non può ciclare e la sua terminazione
è quindi garantita.
dimostrazione:
Si assuma, per assurdo,
che il metodo cicli producendo la
sequenza di dizionari:
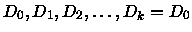 .
Una variabile sarà detta oscillante
se in base per alcuni di questi dizionari
ma fuori base per altri.
Sia t il massimo indice per il quale xt è oscillante.
Nella sequenza
.
Una variabile sarà detta oscillante
se in base per alcuni di questi dizionari
ma fuori base per altri.
Sia t il massimo indice per il quale xt è oscillante.
Nella sequenza
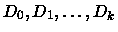 avremo pertanto un dizionario D che
vede xt come variabile uscente
(in base per D ma fuori base nel dizionario seguente)
e sia xs la variabile entrante
in base al posto di xt.
Ovviamente la sequenza
avremo pertanto un dizionario D che
vede xt come variabile uscente
(in base per D ma fuori base nel dizionario seguente)
e sia xs la variabile entrante
in base al posto di xt.
Ovviamente la sequenza
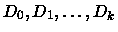 dovrà inoltre contenere un dizionario D* con xt rientrante in base.
Se B è l'insieme degli indici delle
variabili in base per D allora possiamo
accennare la struttura di D:
dovrà inoltre contenere un dizionario D* con xt rientrante in base.
Se B è l'insieme degli indici delle
variabili in base per D allora possiamo
accennare la struttura di D:
Naturalmente la funzione
obiettivo z assumerà
lo stesso valore nelle soluzioni di base
associate a D e D*.
Pertanto l'ultima riga del dizionario D*potrà essere scritta come:
dove cj* = 0 ogniqualvolta xj è in base per D*.
Poichè quest'ultima equazione è stata ottenuta
dalle equazioni descriventi D tramite operazioni di pivot
essa deve ammettere ogni soluzione ammessa da Ded in particolare deve risultare soddisfatta
dalla scelta dei seguenti valori:
Pertanto avremo
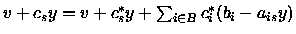 che convenientemente raccogliendo y diviene:
che convenientemente raccogliendo y diviene:
E poichè il secondo termine di quest'equazione
è una costante indipendente da ypossiamo concludere che
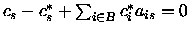 .
D'altro canto cs > 0 poichè xs è entrante in D.
Inoltre
.
D'altro canto cs > 0 poichè xs è entrante in D.
Inoltre
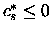 poichè s < t e tuttavia
xt e non xs è la variabile entrante in D*.
Possiamo pertanto concludere che
poichè s < t e tuttavia
xt e non xs è la variabile entrante in D*.
Possiamo pertanto concludere che
Siccome
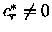 la variabile xr non è in base
per D* ed è quindi oscillante.
Tuttavia
la variabile xr non è in base
per D* ed è quindi oscillante.
Tuttavia 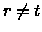 dato che
ct* ats > 0:
siccome xt entra in D* allora ct* > 0;
siccome xt esce da D allora
ats > 0.
Pertanto r < t e siccome xr non entra in D*al posto di xt ne deduciamo che cr* non può essere positivo.
Quindi
dato che
ct* ats > 0:
siccome xt entra in D* allora ct* > 0;
siccome xt esce da D allora
ats > 0.
Pertanto r < t e siccome xr non entra in D*al posto di xt ne deduciamo che cr* non può essere positivo.
Quindi
Poichè tutte le iterazioni che compongono il ciclo
sono degeneri, a D e D* è di fatto
associata la stessa soluzione.
In particolare xr, che è fuori base per D*,
avrà valore nullo anche nella soluzione
associata a D e pertanto br = 0.
Quindi xr era candidata
a lasciare la base in D e contrariamente alla regola dell'indice minimo
le abbiamo preferito xt.
Q.E.D.
Homeworks proposti
Il metodo del simplesso
in due fasi,
implementato utilizzando una qualsiasi
strategia che ne garantisca la terminazione
(come per esempio la regola di Bland),
costituisce dimostrazione algoritmica
del seguente risultato:
Teorema 2 (Teorema Fondamentale della Programmazione Lineare)
Ogni problema di PL in forma standard ha le seguenti tre proprietà:
- (i)
- Se non ha una soluzione ottimale
allora è o inammissibile o illimitato.
- (ii)
- Se ha una soluzione ammissibile
allora ha una soluzione ammissibile di base.
- (iii)
- Se ha una soluzione ottimale
allora ha una soluzione ottimale di base.
Argomentare più precisamente
il Teorema Fondamentale della Programmazione Lineare,
sulla base del comportamento
del metodo del simplesso in due fasi
e dei suoi possibili esiti.
Buon Lavoro!
|
6 Marzo 1998
|
© Dipartimento di Matematica - Università di Trento

|