 |
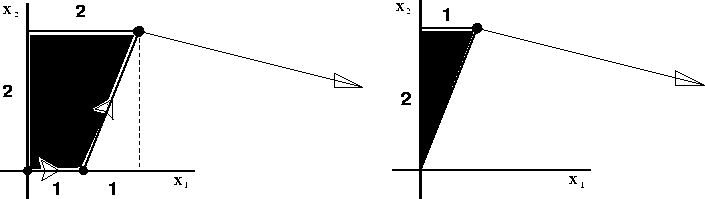
| Figure 1: Due controesempi, il secondo essenziale. |
Contenuto della lezione del 5 Marzo 1998
L'homework proposto la volta scorsa
consisteva nel produrre un controesempio
alla seguente congettura:
se ad una certa iterazione del metodo
del simplesso il costo ridotto relativo ad una variabile
non in base é negativo allora
posso concludere che quella variabile
sarà ancora non in base al raggiungimento della soluzione ottimale.
Sfruttando la visione geometrica siamo di fatto andati a proporre due controesempi a questa congettura. Gli spazi delle soluzioni ammissibili ed il gradiente della funzione obbiettivo sono rappresentati, per questi due problemi, in figura.
Dalla rappresentazione nel piano
siamo quindi risaliti alla formulazione
algebrica dei due problemi che abbiamo poi risolto con
il metodo del simplesso verificando come essi
disprovassero effettivamente la congettura in questione.
Nel seguire questo percorso, e limitatamente al secondo esempio, abbiamo tuttavia individuato un'anomalia nel metodo del simplesso e l'abbiamo battezzata degenerazione. Nonostante questo fenomeno di degenerazione il metodo riusciva comunque a portarci alla soluzione ottimale. Era però d'obbligo a questo punto chiedersi se questa anomalia non potesse inficiare la validità del metodo e far sì che esso non terminasse su alcuni problemi particolarmente sfortunati. La risposta è stata SI`: il metodo del simplesso può andare in ciclo. Abbiamo proposto una strategia per ridurre la probabilitá di degenerare e quindi di ciclare: il metodo delle perturbazioni. Abbiamo dato un esempio dove un'implementazione semplicistica del metodo delle perturbazioni non risulta sufficiente ad evitare di andare in ciclo. (L'esempio é quello riportato quì sotto come homework.) Si è quindi intodotto il metodo lessicografico come implementazione accorta del metodo delle perturbazioni. Si é dimostrato che con il metodo lessicografico la degenerazione non può più avere luogo. Pertanto l'impiego del metodo lessicografico impedisce al metodo del simplesso di entrare in ciclo e ne garantisce quindi la terminazione.
Homeworks proposti
Nel seguente problema di PL la quantità
![]() è stata introdotta
come piccola perturbazione al fine di
ridurre la probabilitá di degenerazione.
Mostrare che nonostante ciò il metodo
del simplesso non solo si trova in presenza
di degenerazione ma addirittura va in ciclo.
è stata introdotta
come piccola perturbazione al fine di
ridurre la probabilitá di degenerazione.
Mostrare che nonostante ciò il metodo
del simplesso non solo si trova in presenza
di degenerazione ma addirittura va in ciclo.
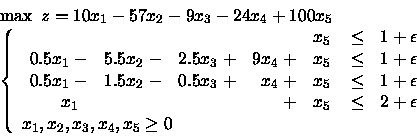
Buon Lavoro!
| 5 Marzo 1998 |
© Dipartimento di Matematica - Università di Trento
|