Homeworks proposti in data 3 Marzo 1998

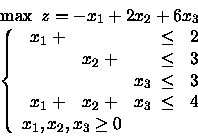
Contenuto della lezione del 3 Marzo 1998

Abbiamo riesposto il metodo del simplesso cercando di astrarre dal singolo problema ed utilizzando la nozione di ``dizionario'' introdotta da J. E. Strum ed utilizzata da Chvtal. Abbiamo poi mostrato come il metodo del simplesso si muova di vertice in vertice nel politopo delle soluzioni ammissibili fino a rangiungere la soluzione ottimale.

L'esempio utilizzato in classe per illustrare il comportamento geometrico del simplesso nello spazio delle variabili di decisione era il problema di decidere se impiantare Canada o Renette Golden. Questo problema agrario era giá stato utilizzato come esempio introduttivo alla PL. Vorrei qui utilizzare un secondo esempio tratto dal libro ``Elementi di Programmazione Matematica'' di F. Maffioli.

Si consideri il seguente problema di PL:

              $$\begin{array}{l} \max \mbox{\ }z = -x_1 + 2x_2 + 6x_3 \\ \... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

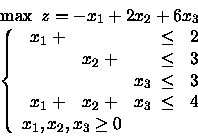
Il poliedro delle soluzioni ammissibili risulta come intersezione di un numero finito di sottospazi affini e quindi convessi ed è pertanto anch'esso convesso. In questo caso particolare é poi limitato ed è quindi un politopo che noi andiamo a rappresentare in figura.

  

Figura 1: Il politopo delle soluzioni ammissibili.

Se lo studente vorrà ora provare, a titolo di esercizio, a risolvere il problema di PL sopra introdotto attraverso l'uso del metodo del simplesso visto in classe, potrà verificare che l'algoritmo del simplesso lo porterà a visitare come soluzioni basiche ammissibili l'insieme dei vertici toccati dal cammino suggerito in figura.

  

Figura 2: Come si muove il metodo del simplesso.

Homeworks proposti

Al termine della lezione precedente un allievo aveva posto la seguente domanda: supponiamo che ad una certa iterazione del metodo del simplesso il costo ridotto relativo ad una variabile non in base x_t sia negativo. Posso concludere allora che quella variabile sarà ancora non in base al raggiungimento della soluzione ottimale?

La risposta a questa domanda é NO. Inoltre, sfruttando forse la visione geometrica che siamo andati formandoci su come lavori il metodo del simplesso, non dovrebbe esservi difficile produrre un controesempio con due sole variabili di decisione.

Buon Lavoro!