Esercizi in preparazione alla provetta sulla PL

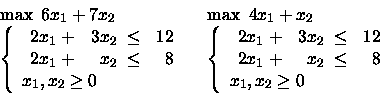
Consiglio innanzittutto di riprendere in mano gli esercizi già proposti e risolti a suo tempo e di cercare di rivederli da nuove angolazioni. Si ricordi ad esempio il PROBLEMA 1 tra i ``Problemi matematici per agricoltori'' nel documento ``Ma questo non è che un semplice problema di PL !!!''.

PROBLEMA 1: Un contadino dispone di 2 ettari di terreno. Il contadino non può dedicare più di 5 mesi l'anno alla cura dei suoi campi. Un ettaro coltivato a Renette Golden gli richiede 3 mesi di lavoro mentre un ettaro coltivato a Canada richiederebbe solamente 2 mesi di lavoro all'anno. Tuttavia un ettaro coltivato a Renette Golden frutterebbe 5 soldi ogni anno contro i 4 soldi ricavabili dallo stesso ettaro se coltivato a Canada. Dovendo decidere come impiantare il terreno, quale politica consentirebbe al contadino di massimizzare il suo guadagno? Formulare il problema secondo il modello della PL.

Quello che consiglio di fare è di soffermarsi su di uno stesso problema ponendosi ulteriori domande ed esercitando un po' tutte le tecniche apprese. Ad esempio: risolvere il problema con il metodo del simplesso ma anche per via geometrica (visto che presenta due sole variabili di decisione). Formulare il problema duale. Ottenere la soluzione del problema duale dall'ultimo dizionario scritto nel risolvere il problema primale, ma eventualmente anche con il metodo del simplesso o per via geometrica (visto che anche il duale presenta due sole variabili di decisione). Fornire un'interpretazione per la variabili duali ed utilizzare la soluzione duale per argomentare l'ottimalità della soluzione primale. Utilizzare gli scarti complementari per ottenere una soluzione duale ottima a partire dalla soluzione primale ottima e viceversa. Considerare singole possibili variazioni al problema ed analizzare come la soluzione ottimale venga a modificarsi. Conviene affittare terreno? A che prezzo? Conviene affittare manodopera, oppure conviene dedicare il proprio tempo ad attività più fruttuose? Qualora la risposta ad una di queste domande dovesse risultare positiva potremmo introdurre una nuova variabile di decisione (quantità di terreno affittato, numero ore contrattate) ed i relativi vincoli. Potremmo cercare di risolvere il problema così ottenuto partendo dalla soluzione ottima già in nostro possesso (se rimasta ammissibile). Ma potremmo anche aggiungere vincoli che distruggano l'ammissibilità della soluzione ottima trovata. Questo è ciò che di fatto accade in pratica, dove spesso la formulazione completa viene a delinearsi solo dopo alcuni tentativi di soluzione e la ``bocciatura'' degli ottimi di seguito ottenuti, poichè una volta espressi si realizza che essi non sono invero accettabili e quindi si aggiungono dei vincoli. Come è ora possibile avvalersi del lavoro svolto sulla formulazione precedente? Aggiungere vincoli distrugge infatti l`ammissibilità della soluzione primale. E per quanto riguarda l'ammissibilità duale, cosa succede?

Se assumerete quest`approccio non dovrebbe mancarvi il materiale su cui esercitarvi. Propongo tuttavia qualche spunto ulteriore.

Risolvere i seguenti problemi salvando lavoro ove possibile

PROBLEMA 1:

$$\begin{array}{l} \max \mbox{\ }6x_1 + 7x_2\\ \left\{ \beg... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

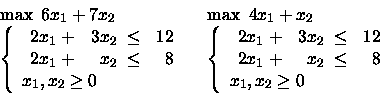
PROBLEMA 2:

$$\begin{array}{l} \max \mbox{\ }x_1 + x_2 + x_3 \\ \left\{ ... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

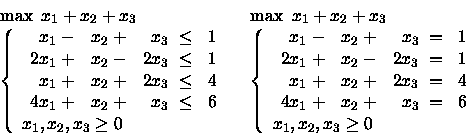
PROBLEMA 3:

$$\begin{array}{l} \max \mbox{\ }2x_1 -3x_2 + 5x_3 \\ \left\... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

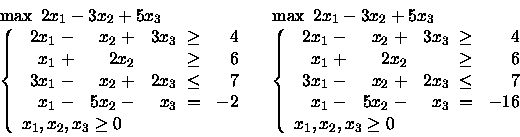
Si noti che l'ultimo vincolo è del tipo x₁-5x₂-x₃ = c. Quale è il più grande valore di c che rende il problema ammissibile?

Spazi di soluzioni

PROBLEMA 4:

Trovare lo spazio delle soluzioni ottimali ed elencare tutte le soluzioni ottimali di base.

$$\begin{array}{l} \max \mbox{\ }2x_1 +x_2 \\ \left\{ \begi... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

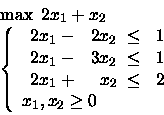
PROBLEMA 5:

$$\begin{array}{l} \max \mbox{\ }2x_1 +x_2 \\ \left\{ \begi... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

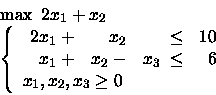
Trovare quindi le soluzioni ottimali che massimizzano -2x₁-x₂-x₃.

Modifiche alla formulazione

PROBLEMA 6:

$$\begin{array}{l} \max \mbox{\ }x_1 +x_2 +x_3\\ \left\{ \b... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

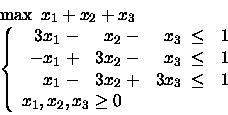
Cosa succede omettendo il secondo vincolo?

PROBLEMA 7:

$$\begin{array}{l} \max \mbox{\ }x_1 +x_2 \\ \left\{ \begin... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

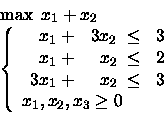
Cosa succede omettendo il primo vincolo? Cosa succede omettendo il secondo vincolo?

PROBLEMA 8:

$$\begin{array}{l} \max \mbox{\ }6x_1 +8x_2 +7x_3\\ \left\{ ... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

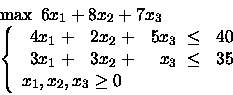
Aggiungere quindi il vincolo $x_1+4x_2+3x_3\leq 30$.

PROBLEMA 9:

$$\begin{array}{l} \max \mbox{\ }x_1 +2x_2 +3x_3 +2x_4\\ \le... ... x_1, x_2, x_3, x_4 \geq 0 \end{array} \right. \end{array}$$

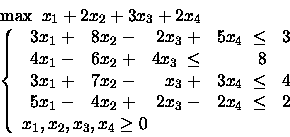
Aggiungere quindi i vincoli $2x_1-x_2+5x_3 +x_4\leq 16$ e $x_1-2x_2-3x_3 +4x_4\geq -8$.

PROBLEMA 10:

$$\begin{array}{l} \max \mbox{\ }2x_1 +x_2 \\ \left\{ \begi... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

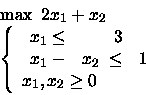
Aggiungere quindi i vincoli $x_1, x_2 \leq 1$.

PROBLEMA 11:

$$\begin{array}{l} \max \mbox{\ }x_1 +x_2 +x_3 +x_4 +x_5 +x_6\... ... x_1, x_2, x_3, x_4 \geq 0 \end{array} \right. \end{array}$$

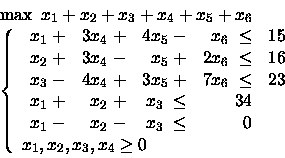
Risolverlo ignorando prima gli ultimi due vincoli.

Scarti Complementari

PROBLEMA 12:

$$\begin{array}{l} \max \mbox{\ }x_1 +x_2 -3x_3 -2x_4\\ \lef... ... x_1, x_2, x_3, x_4 \geq 0 \end{array} \right. \end{array}$$

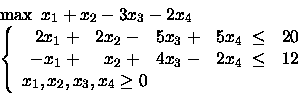
Considerare la soluzione x₁ = x₂ = 5 e x₃ = x₄ = 0. La soluzione proposta è ammissibile? È di base? È ottima? PROBLEMA 13:

$$\begin{array}{l} \max \mbox{\ }4x_1 +5x_2 -3x_3 -8x_4\\ \l... ... x_1, x_2, x_3, x_4 \geq 0 \end{array} \right. \end{array}$$

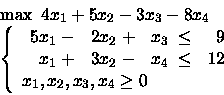
Considerare la soluzione x₁ = x₂ = 3 e x₃ = x₄ = 0. La soluzione proposta è ammissibile? È di base? È ottima?

PROBLEMA 14:

$$\begin{array}{l} \max \mbox{\ }3x_1 +4x_2 +2x_3 +5x_4\\ \l... ... x_1, x_2, x_3, x_4 \geq 0 \end{array} \right. \end{array}$$

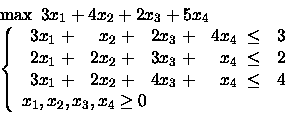
L'uccellino mi ha detto che nella soluzione ottimale le variabili x₂ ed x₄ sono strettamente positive e che inoltre il terzo vincolo è soddisfatto come diseguaglianza stretta. Trovare la soluzione ottimale. Se la funzione obiettivo è il profitto di un`attività, quanto saremmo disposti a pagare per incrementare di un'unità il termine noto nel primo, secondo o terzo vincolo? E fino a dove saremmo disposti a pagare tale prezzo? Di quanto dovremmo alterare ciascun coefficiente nella funzione obiettivo (singolarmente) affinchè la soluzione non sia più ottima?

Buon Lavoro!