Alcuni Problemi Combinatorici su Grafi --- Parte Seconda

Alcuni Problemi Combinatorici su Grafi

Parte Seconda

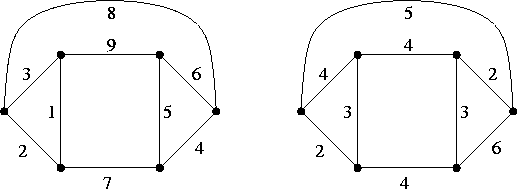
Di ciascuno dei seguenti grafi dire se è planare (e motivare), bipartito (e motivare). In ciascuno dei seguenti grafi trovare un albero ricoprente di peso minimo.

Nei due seguenti grafi trovare un accoppiamento perfetto di peso minimo e fornire un certificato di ottimalità.

$\begin{figure}% \begin{center} \leavevmode \psfig{figure=match1.eps, height=4.2 true cm}\par\end{center}\end{figure}$

Nei due seguenti grafi trovare un accoppiamento perfetto di peso minimo e fornire un certificato di ottimalità.

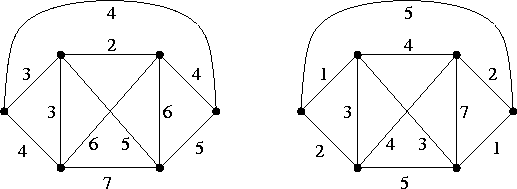
$\begin{figure}% \begin{center} \leavevmode \psfig{figure=match2.eps, height=4.2 true cm}\par\end{center}\end{figure}$

Nei due seguenti grafi trovare un accoppiamento perfetto di peso minimo e fornire un certificato di ottimalità.

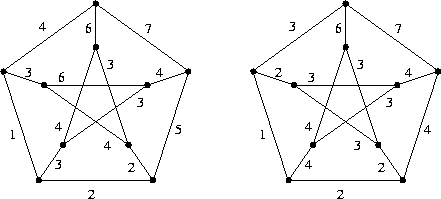
$\begin{figure}% \begin{center} \leavevmode \psfig{figure=P.eps, height=4.4 true cm}\par\end{center}\end{figure}$

Nel grafo seguente trovare un accoppiamento di cardinalità massima e produrre un certificato di ottimalità. Trovare inoltre un accoppiamento di peso massimo e relativo certificato di ottimalità.

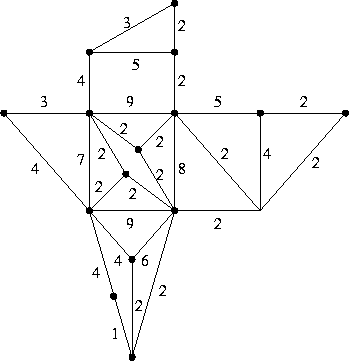
$\begin{figure}% \begin{center} \leavevmode \psfig{figure=max.eps, height=8 true cm}\par\end{center}\end{figure}$

Nel grafo seguente trovare un accoppiamento perfetto di peso minimo e fornire un certificato di ottimalità.

$\begin{figure}% \begin{center} \leavevmode \psfig{figure=big.eps, height=7.2 true cm}\par\end{center}\end{figure}$

8 Maggio 1998