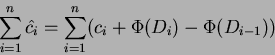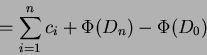Next: Gli Heap
Up: Analisi della Complessità Ammortizzata
Previous: Analisi della Complessità Ammortizzata
Indice
Data una struttura dati e una sequenza di 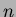 operazioni su di essa, si definisca come
operazioni su di essa, si definisca come 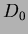 la struttura
iniziale, per
la struttura
iniziale, per 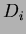 la struttura dati che si ottiene eseguendo l'
la struttura dati che si ottiene eseguendo l'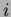 -esima operazione sulla struttura
-esima operazione sulla struttura 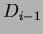 .
Per ogni
.
Per ogni
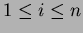 , sia
, sia 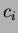 é il costo effettivo della
é il costo effettivo della 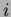 -esima operazione della sequenza. È possibile
definire una funzione potenziale (o più semplicemente potenziale)
-esima operazione della sequenza. È possibile
definire una funzione potenziale (o più semplicemente potenziale) 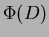 che associa allo stato
della struttura un numero reale detto appunto potenziale1.
che associa allo stato
della struttura un numero reale detto appunto potenziale1.
Il costo ammortizzato è cosí definito:
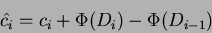
Il costo ammortizzato delle 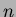 operazioni quindi sará:
operazioni quindi sará:
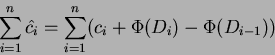
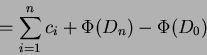
Per garantire che
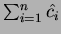 domini il costo effettivo totale deve valere che
domini il costo effettivo totale deve valere che
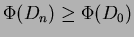 cioè che l'analisi della complessità è terminata con un ``credito'' anzichè con un
``debito''.
cioè che l'analisi della complessità è terminata con un ``credito'' anzichè con un
``debito''.
Non essendo sempre noto il numero di operazioni che potrebbero essere eseguite, è indispensabile garantire che
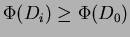 per tutti i valori di
per tutti i valori di 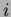 . Per semplicità spesso si definisce
. Per semplicità spesso si definisce 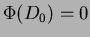 e basta poi
dimostrare che
e basta poi
dimostrare che
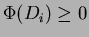
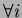 per essere sicuri di avere ottenuto un limite superiore al costo
effettivo totale.
per essere sicuri di avere ottenuto un limite superiore al costo
effettivo totale.
- Esempio(Operazioni su pile):
si consideri una pila con le operazioni Push, Pop e MultiPop e si
definisca
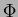 come il numero di elementi presenti nella pila. Si osservi come
come il numero di elementi presenti nella pila. Si osservi come 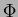 sia funzione del solo
stato della struttura dati, ossia
sia funzione del solo
stato della struttura dati, ossia 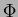 è effettivamente una funzione potenziale.
Nel caso iniziale la pila è
vuota e si ha
è effettivamente una funzione potenziale.
Nel caso iniziale la pila è
vuota e si ha 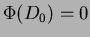 ; dopo un numero indefinito
; dopo un numero indefinito 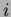 di operazioni il potenziale è
di operazioni il potenziale è
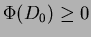 .
Questo fatto, come detto in precedenza, garantisce che il costo ammortizzato totale di n operazioni rispetto alla
funzione potenziale
.
Questo fatto, come detto in precedenza, garantisce che il costo ammortizzato totale di n operazioni rispetto alla
funzione potenziale 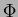 domini il costo effettivo delle operazioni stesse.
domini il costo effettivo delle operazioni stesse.
Definiamo 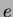 il numero di elementi presenti nella pila.
il numero di elementi presenti nella pila.
Non resta che calcolare i costi ammortizzati delle varie operazioni:
- Push:
- se la
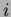 -esima operazione è una Push si ha:
-esima operazione è una Push si ha:
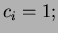
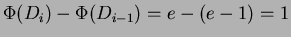 ;
;
Sostituendo in
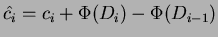 si ha:
si ha:
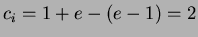 ;
;
Il costo ammortizzato è costante.
- Pop:
- se la
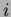 -esima operazione è una Pop si ha:
-esima operazione è una Pop si ha:
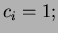
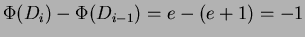 ;
;
Sostituendo in
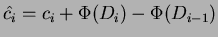 si ha:
si ha:
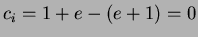 ;
;
Il costo ammortizzato é costante.
- MultiPop:
- se la
 -esima operazione è una MultiPop si ha:
-esima operazione è una MultiPop si ha:
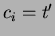 dove
dove 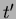 e` il numero di elementi tolti alla pila;
e` il numero di elementi tolti alla pila;
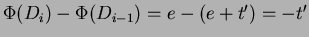 ;
;
Sostituendo in
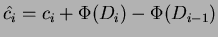 si ha:
si ha:
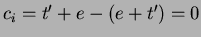 ;
;
Il costo ammortizzato è costante.
Il costo ammortizzato di tutte e tre le operazioni é 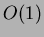 , quindi il costo di una
qualsiasi sequenza di
, quindi il costo di una
qualsiasi sequenza di 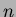 operazioni é
operazioni é 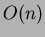 .
.




Next: Gli Heap
Up: Analisi della Complessità Ammortizzata
Previous: Analisi della Complessità Ammortizzata
Indice
Paolo Larcheri
2002-01-26