Solution to an homework proposed on December 6, 2001

First Homework (from the second round of homeworks)

On December 6, we mentioned that the Two Phases Simplex Method, implemented by employing any strategy which guarantees termination (like Bland's pivoting rule or resorting on sound perturbation methods like for example the lexicographic method) gives algorithmic proof of the Fundamental Theorem of Linear Programming. We asked as homework to read out this algorithmic proof.

Theorem 0.1 (The Fundamental Theorem of Linear Programming)   Each LP problem in standard form enjoies the following three properties:

(i)

if it has no optimal solution, then it is either infeasible or unbounded;

(ii)

if it is feasible, then it has a basic feasible solution;

(iii)

if it has an optimal solution, then it has a basic optimal solution.

Proof: Given any LP problem in standard form, run on it the two phases simplex method implemented by employing any strategy which guarantees termination. When termination occurs this can have happened only for 3 possible reasons:

(A)

we end up the first phase by discovering that the original problem is infeasible;

(B)

termination occurs in the second phase while detecting unboundedness;

(C)

termination occurs in the second phase while detecting optimality of the current basic solution.

Now, if the problem is neither infeasible nor unbounded, then neither (A) nor (B) can occur. Hence, since termination is guarantee, we know that (C) eventually occurs, hence the problem admits a basic optimal solution. This accounts for $(i)$ and $(iii)$. Can you now prove $(ii)$?

Second Homework (from the second round of homeworks)

We asked to consider the following possible strengthening of the Fundamental Theorem just above.

Conjecture 0.2 (A strengthening of the Fundamental Theorem of Linear Programming)   Each LP problem enjoies the following three properties:

(i)

if it has no optimal solution, then it is either infeasible or unbounded;

(ii)

if it is feasible, then it has a basic feasible solution;

(iii)

if it has an optimal solution, then it has a basic optimal solution.

We posed the following question:

Which one of (i), (ii) and (iii) does still hold?

We can easily argue that (i) does still hold as follows:

Assume given any LP problem $P$. We know that we can put $P$ in standard form, which means that we can derive an LP problem $P'$ with the property that $P'$ has an optimal solution of value $z$ (or is infeasible, or is unbounded) if and only if $P$ has an optimal solution of value $z$ (or is infeasible, or is unbounded, respectively). Apply the Fundamental Theorem to $P'$.

To show that neither (ii) nor (iii) can be given for granted without the assumption of the problem <b>being in standard form</b>, just consider an LP problem in 2 dimensions whose feasible set is a line.

This will certainly be a counterexample for (ii) since the feasible set is non-empty, yet we have no vertices, hence no feasible solutions.

But to make it a counterexample to (iii) you must choose you objective function carefully. Can you propose the right objective function to make it a counterexample to (iii) as well?

Can you propose a counterexample for 3 dimensions?

I am just curious two know whether in your counterexample for 3 dimensions the feasible set was a 2-dimensional object or an 1-dimensional one.

Third Homework (from the second round of homeworks)

We finally proposed the following problem.

With the insight gained at the previous point, can you now prove the Fundamental Theorem of Linear Programming by direct arguments, without relying on the simplex method?

I do not want to spoil your fun, hence I will ask you to fill in the steps in the following proof:

Step 1: please, define formally what it means for a polyhedron $P$ to contain a line;

Step 2: please, formalize the arguments in the picture to obtain a proof ( = convince yourself of the truth) of the following theorem.

Theorem 0.3   Suppose that the polyhedron $P=\{x\in {\rm I\!R}^n \, : A x \geq b\}$ is nonempty. Then, if $P$ does not contain a line, then $P$ has a basic feasible solution.

Figure 1: Starting from an arbitrary point of a polyhedron, we choose a direction along which all currently active constraints remain active. We then move along that direction until a new constraint is about to be violated. At that point, the number of linearly independent active constraints has increased by at least one. We repeat this procedure until we end up with $n$ linearly independent active constraints, at which point we have a basic feasible solution.

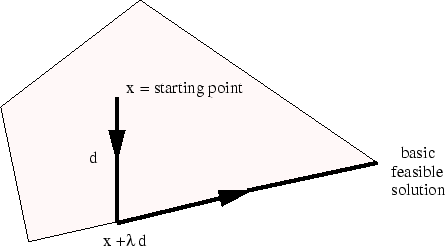Step 3: please, derive the following corollary.

Corollary 0.4   Every nonempty bounded polyhedron and every nonempty polyhedron in standard form has at least one basic feasible solution.

Let me pose you another intriguing, this time algorithmic, question. We proposed to use the simplex method on the auxiliary problem to find a first basic feasible solution to the original problem (or detect that such problem is infeasible).

Algorithmic Problem: Can you turn the proof sketched into the above picture into a polynomial time algorithm which, starting from a feasible solution to an LP problem, produces a basic feasible solution for the same problem?

Question: If you settled the above algorithmic problem on the positive, does this mean that you can trow the two phase simplex method into the garbige can? Why not (if not)?