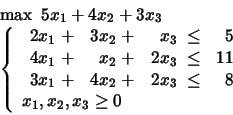
Homeworks proposed on 4 December 2001

Content of the class on 4 December 2001

We have exposed how the simplex method works. While working on specific examples, we have tried to abstract from the single problem. Our exposition was based on the notion of ``dictionary'' as introduced by J. E. Strum and promoted by Chvtal. First, we used the simplex method to solve the following LP problem:

$$\begin{array}{l} \max \mbox{\ }5x_1 + 4x_2 + 3x_3 \\ \le... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

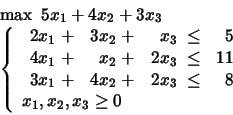
A first homework

Use the simplex method to solve the following LP:

$$\begin{array}{l} \max \mbox{\ }3x_1 + 2x_2 + 4x_3 \\ \le... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

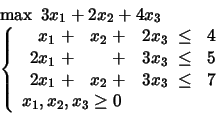
More on the content of the class on 4 December 2001

We have also considered examples in which no optimal solution is present because the polyhedron is unbounded. Moreover, we have also faced the problem of finding an initial feasible basic solution from which to start (or realize that the problem is infeasible).
Finally, we have also observed how the simplex method moves from vertex to vertex of the polyhedron of feasible solutions until it reaches an optimal solutions. But let us monitor this behaviour on a more complex example taken from the book ``Elementi di Programmazione Matematica'' of F. Maffioli.

Let us consider the following LP problem:

$$\begin{array}{l} \max \mbox{\ }z = -x_1 + 2x_2 + 6x_3 \\ ... ...y} \\ x_1, x_2, x_3 \geq 0 \end{array} \right. \end{array}$$

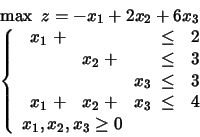
The polyhedron of the feasible solutions is the intersection of a finite number of halfplanes. These halfplanes are convex, hence the polyhedron is also convex. In this special case the polyhedron is also bounded, hence is a politope. We draw the politopo of feasible solutions in the following picture.

Figure: The politopo of feasible solutions.

If you now try, as an exercise, to solve the above LP problem by means of the simplex method, you will have the opportunity to verify that the algorithm will lead you to visit as feasible basic solutions, the sequence of vertices as visited by the path indicated in the picture.

Figure: How the simplex method moves from vertex to vertex.

A second homework

During the class, the following question came about: assume that at a given iteration of the simplex method the reduced cost relative to a non-basic variable $x_i$ is negative. Can I then conclude that $x_i$ will still be non-basic when the optimal solution is reached?

As I already anticipated, the answer to an even weaker conjecture is NO. Moreover, exploiting the geometric view by now developed on the way the simplex method moves about, it should now be possible to buid up a counterexample (even with only 2 decision variables).

Enjoy!