Solution to an homework proposed on December 29, 2001

On December 29, we asked to produce a counterexample to the following conjecture:

if at a certain iteration of the simplex method, the reduced cost of a non-basic variable is negative, then that variable will not become basic in the sequel.

We will actually provide an even stronger counterexample, where the non-basic variable is forced to be strictly positive in every optimal solution. (This is hence a counterexample to a weaker conjecture, could you formulate this false conjecture nicely?)

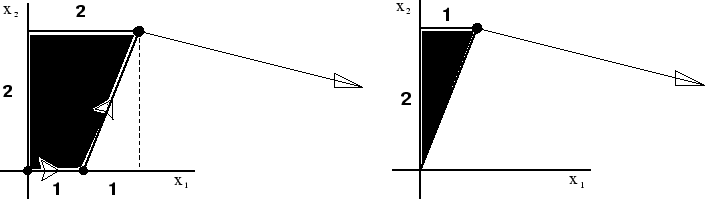
To build up this counterexample, we will rely on the geometric view, which is something that we humans are very gifted to (at least up to almost 3 dimensions). As I anticipated you, in this case 2 dimensions were enough. For example, the feasible reagion and the gradient of the objective function of our counterexample could simply be represented as in the following pictures, where the picture on the left provides a first counterexample, and the one on the right wants to isolate a smallest possible one.

Figure: Two counterexamples, the second is essential.

Note that in the very first dictionary (the one associated to the origin) the reduced cost relative to $x_2$ is negative, and nevertheless $x_2$ is strictly positive in the unique optimal solution to this LP problem.

Can you go from the representation in the plane here above to the algebraic formulation of the above two counterexamples?

Are they counterexamples both in the ``weak'' and in the ``strong'' sense?

Can you verify that they are indeed counterexamples by running the simplex method?

If you have tried to run the simplex method on the algebraic formulation you have provided to the second counterexample, you will have noticed that the first pivot you were forced to take was degenerate (that is, no improvement in objective function nor real change in the associated basic solution came about). Why is the origin a degenerate point for the second counterexample?

How many constraints are active for the origin?

How many dictionaries have the origin as associated basic solution?

Note that the origin is the basic solution associated to the first and to the second dictionaries encountered by the simplex method. But what is the difference among these two dictionaries? Can you tell why from the first dictionary no entering variable could have given us an improvement in objective function?