Let's go exercises with the Simplex Method

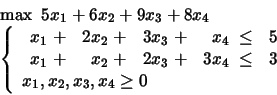
Solve the following LP problems with the Simplex Method

$$\begin{array}{l} \max \mbox{\ }5x_1 + 6x_2 + 9x_3 + 8x_4\\... ... x_1, x_2, x_3, x_4 \geq 0 \end{array} \right. \end{array}$$

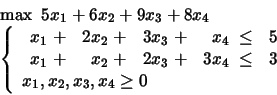
Taken from Chapter 2 of the book ``Linear Programming'' of V. Chvátal.

$$\begin{array}{l} \max \mbox{\ }2x_1 + x_2 \\ \left\{ \b... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

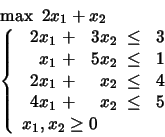
Taken from Chapter 2 of the book ``Linear Programming'' of V. Chvátal.

Understanding the set of all optimal solutions with the Simplex Method

Given the following LP problem, employ the Simplex Method to produce a description of the set of all optimal solutions.

$$\begin{array}{l} \max \mbox{\ }2x_1 + 3x_2 + 5x_3 + 4x_4\\... ... x_1, x_2, x_3, x_4 \geq 0 \end{array} \right. \end{array}$$

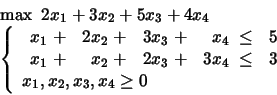
Taken from Chapter 2 of the book ``Linear Programming'' of V. Chvátal.

How to obtain an initial feasible solution

Solve the following LP problems introducing first the respective auxiliary problems and employing the Two Phases Simplex Method.

$$\begin{array}{l} \max \mbox{\ }3x_1 + x_2 \\ \left\{ \b... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

$$\begin{array}{l} \max \mbox{\ }3x_1 + x_2 \\ \left\{ \b... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

$$\begin{array}{l} \max \mbox{\ }3x_1 + x_2 \\ \left\{ \b... ...{array} \\ x_1, x_2 \geq 0 \end{array} \right. \end{array}$$

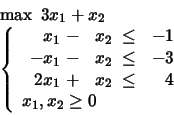
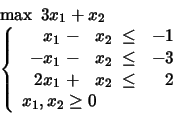
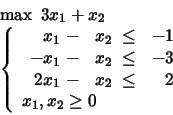
Taken from Chapter 3 of the book ``Linear Programming'' of V. Chvátal.

Have fun!