Exercises: Bipartite Matching and Beyond

Exercises: Bipartite Matching and Beyond

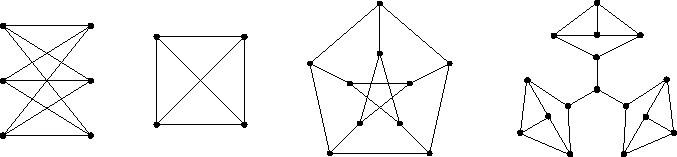
For all of the following graphs tell whether they are bipartite and provide a certificate for your answer.

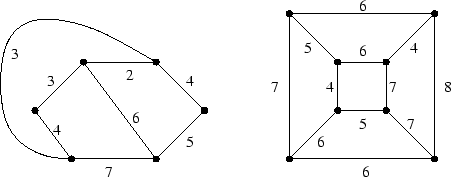
In the following two graphs, find a minimum weight perfect matching and a proof of optimality.

$\begin{figure}% h=here; t=top; b=bottom;\begin{center} \leavevmode \psfig {figure=bipmatch.eps, height=4 true cm}\par\end{center}\end{figure}$

Do the following graphs admit a perfect matching? (motivate) Can I color their edges in three colors? (motivate)

$\begin{figure}% h=here; t=top; b=bottom;\begin{center} \leavevmode \psfig {figure=colore.eps, height=3.5 true cm}\par\end{center}\end{figure}$

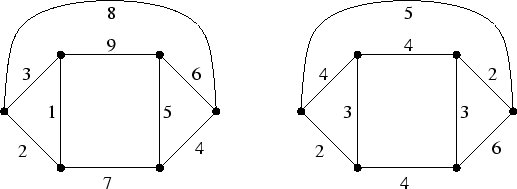
In the following two graphs, find a minimum weight perfect matching and convince me of the optimality of the solutions you propose.

$\begin{figure}% h=here; t=top; b=bottom;\begin{center} \leavevmode \psfig{figure=match1.eps, height=4.2 true cm}\par\end{center}\end{figure}$

2002-01-15