Ma questo non è che un semplice problema di PL !!!


Formulare i seguenti problemi secondo il modello della PL

Problemi matematici per agricoltori

PROBLEMA 1: Un contadino dispone di 2 ettari di terreno. Il contadino non può dedicare più di 5 mesi l'anno alla cura dei suoi campi. Un ettaro coltivato a Renette Golden gli richiede 3 mesi di lavoro mentre un ettaro coltivato a Canada richiederebbe solamente 2 mesi di lavoro all'anno. Tuttavia un ettaro coltivato a Renette Golden frutterebbe 5 soldi ogni anno contro i 4 soldi ricavabili dallo stesso ettaro se coltivato a Canada. Dovendo decidere come impiantare il terreno, quale politica consentirebbe al contadino di massimizzare il suo guadagno? Formulare il problema secondo il modello della PL.


PROBLEMA 2: Una fattoria consiste di due lotti di terreno A e B rispettivamente di 200 e 400 acri. Sei tipi di cereali, numerati da 1 a 6, possono esservi coltivati. Per ogni quintale di cereale il profitto è dato dalla seguente tabella:


cereale 1 2 3 4 5 6
profitto/q 48 62 28 36 122 94

Ogni quintale di cereale necessita di una certa area (in acri) e di una certa quantità d'acqua (in mc) secondo la seguente tabella:


cereale 1 2 3 4 5 6
area su A (acri/q) 0.02 0.03 0.02 0.016 0.05 0.04
area su B (acri/q) 0.02 0.034 0.024 0.02 0.06 0.034
acqua (mc/q) 120 160 100 140 215 180

Il volume totale di acqua disponibile è di 400000 mc. Si vuole massimizzare il profitto. Formulare il problema secondo il modello della PL.

Il secondo problema é tratto dal Capitolo 3 del libro ``Elementi di Programmazione Matematica'' di F. Maffioli.


Il Problema della Dieta e ``Blending Problems''

PROBLEMA 3: Per ben alimentare un certo tipo di animale è necessario fornirgli 4 sostanze base: A, B, C e D. La quantità minima giornaliera che ogni animale richiede é data da: 0,4 kg di A; 0,6 kg di B; 2 kg di C; 1,3 kg di D. Il foraggio è ottenuto mescolando due farine M ed N.

1kg di M contiene: 100 gr di A; nulla di B; 100 gr di C; 100 gr di D.
1kg di N contiene: nulla di A; 100 gr di B; 200 gr di C; 100 gr di D.

Con 1 ECU possiamo comperare 4 kg di M o 8 Kg di N. Formulare il problema di minimizzare i costi secondo il modello della PL e risolverlo per via geometrica e con il metodo del simplesso.

Tratto dal Capitolo 3 del libro ``Elementi di Programmazione Matematica'' di F. Maffioli.

PROBLEMA 4: Un imprenditore manufatturiero vuole produrre una lega che sia 30% piombo, 30% zinco, e 40% stagno. Sul mercato, sono reperibili le leghe A, B, C, ..., con composizioni e costi come espresso dalla seguente tabella.


Lega A B C D E F G H I Mistura Desiderata
% Piombo 10 10 40 60 30 30 30 50 20 30
% Zinco 10 30 50 30 30 40 20 40 30 30
% Stagno 80 60 10 10 40 30 50 10 50 40
Costo [$/lb] 4.1 4.3 5.8 6.0 7.6 7.5 7.3 6.9 7.3 MIN

Ovviamente, l'imprenditore può semplicemente acquistare la lega E da sola ed utilizzarla direttamente, ma essa costa $7.60 per pound. Se egli impiegasse $\frac{1}{4}$ di pound per ciascuna delle leghe A, B, C, D, riuscirebbe ad ottenere 1 pound della composizione 30-30-40 desiderata al costo di $5.05. Dopo alcuni tentativi di questo tipo, l'imprenditore vorrebbe avvalersi di un approccio più sistematico al suo problema. Potresti indicargli come la programmazione lineare possa essere utilizzata per modellare il suo problema e reperire la soluzione ottima? Quanto riesci a fargli risparmiare? Perchè non ti è possibile fare di meglio?


Il Problema del Trasporto

PROBLEMA 5: Una ferriera possiede due miniere e tre impianti per la produzione di acciaio. Gli impianti richiedono rispettivamente 70, 140 e 100 tonnellate di minerale, mentre le miniere producono nello stesso periodo rispettivamente 100 e 200 tonnellate di minerale. La tabella seguente riporta i costi di trasporto dalle miniere agli impianti in lire/tonnellate.

  all'impianto
dalla miniera 1 2 3
1 100 160 250
2 150 300 200

Formulare il problema di minimizzare il costo di trasporto secondo il modello della PL.

Tratto dal Capitolo 3 del libro ``Elementi di Programmazione Matematica'' di F. Maffioli.


Interpolazione lineare di dati sperimentali

PROBLEMA 6: Di una grandezza $y$ dipendente da una variabile $x$ si sono effettuate 6 misure riportate come coppie $(x,y)$ nell'elenco seguente: $(1,16)$ $(2,18)$ $(3,12)$ $(4,7)$ $(5,6)$ $(6,6)$. Si vuole determinare la retta del piano cartesiano che ``meglio'' interpola le sei misure nel senso di minimizzare il massimo scarto tra valore misurato e valore della retta. Modellare come un problema di programmazione lineare.

Più in generale, nell'attività sperimentale accade di considerare il seguente problema. Dato un sistema di equazioni

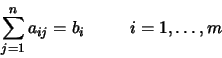
\begin{displaymath} \sum_{j=1}^n a_{ij} = b_i \mbox{\hspace{1cm}} i = 1, \ldots, m \end{displaymath}

con $m > n$, trovare la ennupla di numeri $\bar{x}_1, \ldots, \bar{x}_n$ che ne costituisce la ``miglior'' approssimazione. Tale concetto può precisarsi meglio definendo con

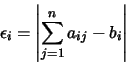
\begin{displaymath} \epsilon_i = \left\vert \sum_{j=1}^n a_{ij} - b_i\right\vert \end{displaymath}

l' errore con cui l'ennupla data soddisfa alla $i$-esima equazione, $i = 1, \ldots, m$. Criteri usati sono quelli dell'errore peggiore ($\max_i e_i$), dell'errore medio ( $\sum_{i=1}^m e_i$) o dell'errore quadratico medio ( $\sum_{i=1}^m {e_i}^2$). Quest'ultimo caso non puó essere inquadrato come un problema di PL. Mostrare come gli altri due casi possano essere ricondotti al modello della PL.

Tratto dal Capitolo 3 del libro ``Elementi di Programmazione Matematica'' di F. Maffioli.


Gestione di Produzione

PROBLEMA 7: Il gestore di una raffineria dispone di 10 milioni di barili di greggio di tipo A e di 6 milioni di greggio di tipo B. La raffineria dispone di tre diversi impianti per produrre sia nafta per riscaldamento (profitto 3 kL/barile) sia benzina (5 kL/barile) con le caratteristiche di rendimento (in barili) riportate in figura:


  Input Output
Impianto A B Benzina Nafta
1 3 5 4 3
2 1 1 1 1
3 5 3 3 4

Formulare il problema di massimizzare il profitto secondo il modello della PL.

Tratto dal Capitolo 3 del libro ``Elementi di Programmazione Matematica'' di F. Maffioli.


PROBLEMA 8: La GELAR produce pacchi di patatine surgelate, sia a bastoncino (A), che in pezzi più piccoli (B) (per le cosidette patate alla svizzera), e di fiocchi (C) (non surgelati) per il purè. La compagnia acquista patate da due produttori (p1 e p2) con rese differenti, riportate nella seguente tabella (l'avanzo del 30 è lo scarto non recuperabile).

produttore A B C
p1 20% 20% 30%
p2 30% 10% 30%

Il profitto della GELAR è di 5 lire per etto di patate provenienti dal produttore 1 e di 6 lire per etto per quelle provenienti dal produttore 2. Ci sono poi delle limitazioni alla quantità di ciascun tipo di prodotto: 6 tonnellate di A, 4 di B e 8 di C. Formulare il problema di massimizzare il profitto secondo il modello della PL e risolverlo per via geometrica e con il metodo del simplesso.

Tratto dal Capitolo 3 del libro ``Elementi di Programmazione Matematica'' di F. Maffioli.


Gestione di Personale

PROBLEMA 9: Un'impresa per la produzione di beni di consumo deve essere gestita in modo da tenere conto delle fluttuazioni della domanda di tali beni su un periodo standard di 6 mesi (gennaio - giugno e luglio - dicembre). I mezzi per adattare l'azienda a tali fluttuazioni sono:

1.
cambiare la quantità di forza lavoro assumendo o licenziando operai;
2.
coprire le punte della domanda con lavoro straordinario;
3.
immagazzinare merce in vista di richieste future.

Ognuna di queste strategie ha le sue limitazioni. La strategia (1) è limitata ad un massimo di 5 operai al mese (sia in più che in meno) con un sovrapprezzo di 500 kL per una nuova assunzione e di 700 kL per ogni licenziamento. La strategia (2) deve tener conto che ogni operaio può al massimo fornire in più 6 unità al mese col lavoro straordinario mentre ne produce 20 regolarmente e che tale prestazione graverà per 30 kL in più per ogni unità di merce prodotta. Ci sono attualmente (inizio semestre) 40 operai ed il magazzino è vuoto: di fatto la politica a lungo termine dell'azienda richieda che il magazzino sia vuoto alla fine di ogni semestre. Le fluttuazioni delle domande previste nei prossimi 6 mesi sono riportate in figura.

mese 1 2 3 4 5 6
unità di merce richiesta 700 600 500 800 900 800

Formulare come un problema di PL.

Tratto dal Capitolo 3 del libro ``Elementi di Programmazione Matematica'' di F. Maffioli.


Buon Lavoro!


2001-12-04 © Dipartimento di Matematica - Università di Trento