But ..., this is just an LP problem !!!


Formulate the following problems within the LP model

Mathematical problems in agriculture

PROBLEM 1: A farmer owns 2 hectars of land. The farmer can not work at his estate for more than 5 months each year. Each hectar planted with Renette Golden (a variety of apples) demands for 3 working months, whereas an hectar planted with the Canada variety demands only 2 working months. However, each hectar planted with Renette Golden currently payes about 5 silver coins whereas the same hectar planted with Canada would fruit 4. Under which planting policy would the farmer maximize his profit? Formulate the problem within the LP model.


PROBLEM 2: A farm is made of two fields: field A has 200 acres, field B has 400 acres. Six kinds of cereals, numbered from 1 to 6, can be cultivated. The profit for each quintal of cereal is given by the following table:


cereale 1 2 3 4 5 6
profitto/q 48 62 28 36 122 94

To produce a quintal of each given cereal we need a certain expanse (in acres) and a certain amount of water (in cubic meters) as specified by the following table:


cereale 1 2 3 4 5 6
area su A (acri/q) 0.02 0.03 0.02 0.016 0.05 0.04
area su B (acri/q) 0.02 0.034 0.024 0.02 0.06 0.034
acqua (mc/q) 120 160 100 140 215 180

The total amount of water that has been put at our disposal is 400000 cubic meters. Formulate the problem of maximizing the profit as an LP problem.


Diet Problems and Blending

PROBLEM 3: To grow up chickens we must supply them, through their diet, 4 fundamental basic ingredients: A, B, C e D. The minimum daily amount for each animal is: 0,4 kg of A; 0,6 kg of B; 2 kg of C; 1,3 kg of D. The pasture is obtained mixing two flours M and N.

1kg of M contains: 100 gr of A; nulla of B; 100 gr of C; 100 gr of D.
1kg of N contains: nulla of A; 100 gr of B; 200 gr of C; 100 gr of D.

With 1 ECU we can buy 4 kg of M or 8 Kg of N. Formulate the problem of minimizing the costs as an LP problem and solve it geometrically and with the simplex method.

PROBLEM 4: A manufacturer wishes to produce an alloy which is 30 per cent lead, 30 per cent zinc, and 40 per cent tin. Suppose there are, on the market, alloys A, B, C, ...with compositions and prices as given in the following table.


Alloy A B C D E F G H I Desired Blend
% Lead 10 10 40 60 30 30 30 50 20 30
% Zink 10 30 50 30 30 40 20 40 30 30
% Tin 80 60 10 10 40 30 50 10 50 40
Costs [$/lb] 4.1 4.3 5.8 6.0 7.6 7.5 7.3 6.9 7.3 MIN

Obviosly, the manufacturer can purchase alloy E alone, but it costs $7.60 per pound. If he buys $\frac{1}{4}$ pound each of alloys A, B, C, D, he gets one pound of a 30-30-40 mixture at a cost of $5.05. After a few trials of this sort, the manufacturer may well seek a more general approach to his problem. Show him as linear programming can be employed to model his problem and find an optimal solution. How much did you spare? Why can't you do better?


A Transportation Problem

PROBLEM 5: An ironworks bases on two mines and three plants to produce steel. With reference to a certain period of time, the plants use 70, 140 and 100 tons respectively of rude ore. In the same period, the mines produce 100 and 200 tons respectively of rude ore. The following table reports the transportation costs from mines to plants in Italian liras per ton.

  all'impianto
dalla miniera 1 2 3
1 100 160 250
2 150 300 200

Formulate the problem of minimizing the transportation cost as an LP problem.


Linear Interpolation of experimental data

PROBLEM 6:

Let $y$ be a magnitude which depends on a variable $x$. When performing measurements on $y$ we record them as $(x,y)$ pairs. Assume for example to have obtained the following 6 measurements: $(1,16)$ $(2,18)$ $(3,12)$ $(4,7)$ $(5,6)$ $(6,6)$. We are interested in finding the line of the Descartes plane which ``best'' interpolates the 6 measurements. As a criterion for ``better'' we are interested in minimizing the maximum discrepance between the measured value and the value on the line. Model as an LP problem.

More generally, in various experimental activities the following problem occurs. Given a system of equations

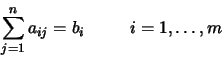
\begin{displaymath} \sum_{j=1}^n a_{ij} = b_i \mbox{\hspace{1cm}} i = 1, \ldots, m \end{displaymath}

with $m > n$, find the $n$ numbers $\bar{x}_1, \ldots, \bar{x}_n$ which give the ``best'' approximation. To specify our criterion for better we define

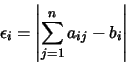
\begin{displaymath} \epsilon_i = \left\vert \sum_{j=1}^n a_{ij} - b_i\right\vert \end{displaymath}

as the error with which the $n$ given numbers model the $i$-th equation, $i = 1, \ldots, m$. At this point, the most used criteria are the following: worst error ($\max_i e_i$), average error ( $\sum_{i=1}^m e_i$) and average least square error ( $\sum_{i=1}^m {e_i}^2$). This very last can not be treated through LP. Show how in the other two cases we can resort on the LP model.


Production Management

PROBLEM 7: You are the production manager of an oil refinery which periodically receives 10 million barrels of crude oil of type A and 6 million barrels of crude oil of type B. The refinery resorts on three different plants to produce naphtha for heating systems (profit 3 kL/barrel) and petrol (5 kL/barile) with the productions (in barrels) as reported in the following table:


  Input Output
Impianto A B Benzina Nafta
1 3 5 4 3
2 1 1 1 1
3 5 3 3 4

Formulate the problem of maximizing the profit as an LP problem.


PROBLEM 8: GELAR produces frozen potatoes in three forms: as sticks (A) (sold as French potatoes), as smaller pieces (B) (sold as Swiss potatoes), as chips (C) (non frozen) for making potatoes muss (Italian purè). The company buys potatoes from two producers (p1 e p2) with different associated production rates, as reported from the following table (the 30% remaining is non-recoverable waste for both producers).

produttore A B C
p1 20% 20% 30%
p2 30% 10% 30%

GELAR makes 5 Italian liras for each hectogram of potatoes coming from producer 1 and 6 liras for each hectogram of potatoes coming from producer 2. There are limitations on the quantity of each kind of product: 6 tons of A, 4 of B and 8 of C. Formulate the problem of maximizing the profit as an LP problem and solve it geometrically and with the simplex method.


Personel Management

PROBLEM 9: A firm has to be managed taking into account the fluctuations in the demands of goods it produces. Assume to work on 6 months periods (January - June and July - December). The ways in which the firm can adapt its assess to these fluctuations are the following:

1.
change its man power by engaging or firing workers;
2.
cover the picks in the demand by relying on overtime work;
3.
store goods in view of future demand.

Each one of these strategies has its own limitations. Strategy 1 is limited up to 5 workers per month (both in hiring and in firing) with an overcost of 500 kL for an hiring and of 700 kL for a firing. With Strategy 2, each worker can give at most 6 units per month of overtime work (while regularly the worker accounts for 20 units) and the overtime cost is of 30 kL more for each unit of goods produced. Right now (beginning of a semester) we have 40 workers and the store is empty: as a matter of fact the policy of the firm requires that the store is empty at the end of each semester. The fluctuations in the demand as forecasted for the next months are given in the following table.

mese 1 2 3 4 5 6
units of goods required 700 600 500 800 900 800

Formulate as an LP problem.


Have Fun!


2001-12-03 © Dipartimento di Matematica - Università di Trento