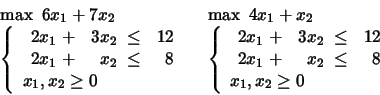
We have by now realized that LP problems, Simplex Methods,
and LP theorems, all have several aspects interwoven in magical and deep ways.
It pays a lot to go back to the first and old exercises
and try to look at them from as many angles as possible.
I am suggesting to first practice all of the ideas you have
encountered on a same single (and simple) problem with the purpouse of giving unity
to what learned until now.
For example,
you could go back to
PROBLEM 1
among the `` Mathematical problems in agriculture''
in the document ``But ..., this is just an LP problem !!!''.
PROBLEM 1:
A farmer owns 2 hectars of land.
The farmer can not work at his estate
for more than 5 months each year.
Each hectar planted with Renette Golden (a variety of apples) demands
for 3 working months,
whereas an hectar planted with the Canada variety
demands only 2 working months.
However, each hectar planted with Renette Golden currently payes
about 5 silver coins whereas the same hectar planted with Canada would
fruit 4.
Under which planting policy would the farmer maximize his profit?
Formulate the problem within the LP model.
What I am suggesting to do is to stop
on a single same old problem and put yourself new questions,
practicing all the spectrum of techniques seen.
For example:
solve the problem with the Simplex Method but also geometrically
(since it only has 2 decision variables you can do it).
Formulate the dual problem.
Grab an optimal solution for the dual problem
from the last dictionary for the primal problem.
You can get to the same dual solution by running the Simplex Method on
the dual, or even geometrically.
Can you provide a meaning for the dual variables
and an interpretation for the dual problem?
On this line, can you argue for the optimality of the primal solution
on the basis of the dual one?
Put the complementary slackness conditions in action
to obtain a dual optimal solution from the primal optimal one,
and viceversa.
Consider possible variations to the problem
and analize how the optimal solution would change.
More precisely, try considering a change in the profits (number of
silver coins for each hectar planted X).
Otherwise, try considering a change in
resources available (number of hectars owned by the farmer and working
months).
The questions you should here consider are for example as follows.
Should the farmer consider renting land?
At which price?
Is it worth renting man-power,
or should the farmer dedicate his own time to more fruitful
activities?
When the answer to such questions is positive,
we could consider introducing new variables
(amount of rented land, working-houers hired)
and the corresponding bounds.
We could here try to solve the problem hence obtained
starting from the old optimal solution or dictionary
(warm start, in case feasibility is preserved).
But it can certainly happen that new constraints kill out
the current solution.
This is what actually happens in practice,
where offen the complete formulation comes gradually to light
only by trials and errors.
(A sequence of optimal solutions is produced,
but they get subsequently trimmed away becouse they lead to
realize new sources of infeasibility).
How is it possible to take advantage of the previous work
in this kind of situations?
Indeed, the addition of new constraints destroyies
primal feasibility.
But what about dual feasibility?
If you will enter this most rewarding approach,
you will soon have abundance of problems on which to practice.
But let me propose some more concrete exercises for making up an
assignment
which you are asked to perform during the Christmas holidays.
Solve the following problems saving as much work as possible
PROBLEM 1:
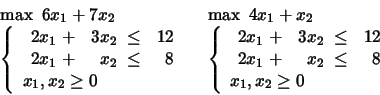
PROBLEM 2:
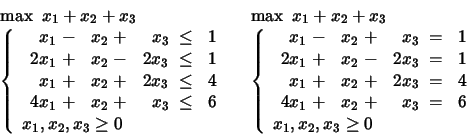
PROBLEM 3:
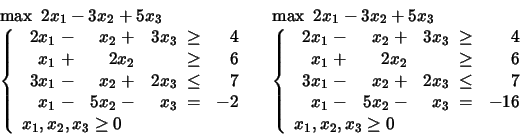
Note that the last constraint is of the form
![]() .
What is the biggest value of
.
What is the biggest value of ![]() which makes the problem feasible?
which makes the problem feasible?
Spaces of Optimal Solutions
PROBLEM 4:
Find the space of optimal solutions
and list all the optimal basic solutions.
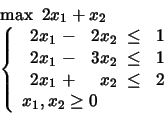
PROBLEM 5:
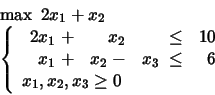
Find next the optimal solutions which maximize
![]() .
.
Dealing with Changes in the Formulation
PROBLEM 6:
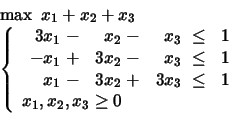
What happens in case the second constraint is dropped?
PROBLEM 7:
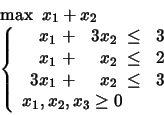
What happens in case the first constraint is dropped? What happens in case the second constraint is dropped?
PROBLEM 8:
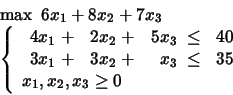
Add next the constraint
![]() .
.
PROBLEM 9:
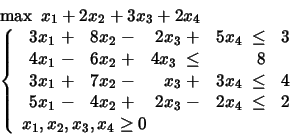
Add next the constraints
![]() and
and
![]() .
.
PROBLEM 10:
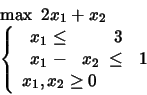
Add next the constraints
![]() .
.
PROBLEM 11:
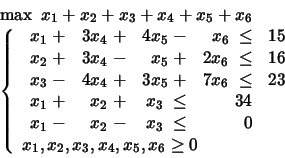
Solve it by first ignoring the last two constraints.
Complementary Slackness
PROBLEM 12:
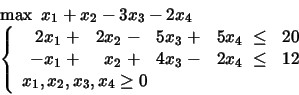
Consider the solution
![]() e
e ![]() .
Is it admissible?
Is it basic?
Is it optimal?
.
Is it admissible?
Is it basic?
Is it optimal?
PROBLEM 13:
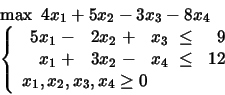
Consider the solution
![]() e
e ![]() .
Is it admissible?
Is it basic?
Is it optimal?
.
Is it admissible?
Is it basic?
Is it optimal?
PROBLEM 14:
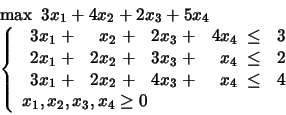
The little bird told me that in the optimal solution
the variables ![]() and
and ![]() are strictly positive
and that the third constraint is satified
with strict inequality (
are strictly positive
and that the third constraint is satified
with strict inequality (![]() ).
Find the optimal solution.
If the optimal solution represents the profit of an activity,
how much would be considering to pay to increment by one unit
the constant in the first, second or third constraint?
And up to what extent would it be reasonable to pay such price?
How much should we alter the single coefficients into the objective
function to destroy optimality of the solution?
).
Find the optimal solution.
If the optimal solution represents the profit of an activity,
how much would be considering to pay to increment by one unit
the constant in the first, second or third constraint?
And up to what extent would it be reasonable to pay such price?
How much should we alter the single coefficients into the objective
function to destroy optimality of the solution?
Enjoy!
| 2001-12-19 |
© Dipartimento di Matematica - Università di Trento
|