

Presentazione
Mantenere ed estrarre velocemente informazioni da un array è una richiesta che capita molto spesso. Molti sottoproblemi si riducono a questo tipo di attività: dalla programmazione dinamica agli algoritmi su grafi, saper determinare velocemente certe grandezze (ad esempio un minimo o una media) circa una certa porzione di dati può essere un passo cruciale.
- Avere una buona intuizione riguardo a ciò che si può o non si può ottenere è molto importante. Risolvere molti problemi aiuta a costruire questa intuizione.
- Nell'ambito di una gara è importante considerare anche la complessità dell'implementazione della struttura.
- Oggi vedremo 4 strutture dati fondamentali di complessità (e potenza) crescente. Saper scegliere la struttura giusta può fare la differenza in gara.
Presentazione
Cosa vedremo oggi
Oggi vedremo:
- Prefix/suffix precomputations
- Fenwick trees
- Sparse tables
- Range trees
Alcuni esempi:
1) Dato un array \(\text{a}[1], \ldots, \text{a}[n]\), trovare \(\text{a}[l] + \cdots + \text{a}[r]\)
2) Lo stesso, ma con point and range updates (online)
3) Dato un array \(\text{a}[1], \ldots, \text{a}[n]\), trovare \(\min\{\text{a}[l], \ldots, \text{a}[r]\}\)
4) Lo stesso, ma con point and range updates (online)
5) Data una permutazione \(\text{a}\) dei numeri da \(1\) a \(n\), trovare il numero di inversioni
6) Dato un array \(\text{a}[1], \ldots, \text{a}[n]\), trovare la più lunga sottosequenza crescente
7) Data una sequenza di bit, supportare le operazioni:
- a) Trovare lo stato di un bit
- b) Negare un sottoarray
8) Data una sequenza di bit, supportare le operazioni:
- a) Trovare il numero di bit settati in un dato sottoarray
- b) Negare un sottoarray
9) Dato un array \(\text{a}[1], \ldots, \text{a}[n]\), supportare le operazioni:
- a) Trovare la posizione del primo valore \(\le x\) in un dato sottoarray
- b) Aggiornare un valore
Informazioni facilmente unibili
IFU
Alcuni esempi di IFU sono:
- Somma, prodotto, xor, min, GCD
- Numero di elementi con valore \(\le x\)
- Valore del massimo sottoarray
1 — Suffix/prefix
precomputations
Suffix/Prefix precomputations
Problema
- Ci viene dato un array di \(n\) interi: \[\text{a}[1], \text{a}[2], \ldots, \text{a}[N]\]
- Ci vengono chieste \(q\) query della forma:
dati \(l\) e \(r\), quanto vale \(\text{a}[l] + \text{a}[l+1] + \cdots + \text{a}[r]\)?
Suffix/Prefix precomputations
La soluzione
- Costruiamo un secondo array \(\text{s}\): \(\text{s}[0], \text{s}[1], \text{s}[2], \ldots, \text{s}[n]\) dove
\(\text{s}[0] = 0\)
\(\text{s}[1] = \text{a}[1]\)
\(\text{s}[2] = \text{a}[1] + \text{a}[2]\)
\(\cdots\)
\(\text{s}[n] = \text{a}[1] + \text{a}[2] + \cdots + \text{a}[n]\) - \(\text{s}[\cdot]\) contiene le somme dei vari prefissi (da cui il nome della tecnica).
- In questo modo \(\text{a}[l] + \cdots + \text{a}[r] = \text{s}[r] - \text{s}[l-1]\).
- Siamo in grado di costruire \(\text{s}\) in tempo \(\mathcal{O}(n)\): basta notare che \[\text{s}[i] = \text{s}[i-1] + \text{a}[i]\quad i=1, \ldots, n.\]
Suffix/Prefix precomputations
Codice
int n, q;
cin >> n >> q;
// Leggi il vettore di input
vector<int> a(n + 1);
for (int i = 1; i <= n; i++)
cin >> a[i];
// Costruisci le somme prefisse
vector<int> s(n + 1);
for (int i = 1; i <= n; i++)
s[i] = s[i - 1] + a[i];
// Processa le query
for (int i = 0; i < q; i++) {
int l, r;
cin >> l >> r;
// Ritorna il valore di a[l] + ... + a[r]
cout << s[r] - s[l - 1] << endl;
}
2 — Fenwick trees
Fenwick trees
Problema
L'idea della prefix/suffix precomputation funziona quando invece della somma siamo interessati ad altre operazioni invertibli, come moltiplicazione e xor. Sfortunatamente, tuttavia, la sua utilità cessa nel momento in cui è necessario prevedere l'aggiornamento dei valori. I Fenwick trees sono in grado di superare questo scoglio.
- Ci viene dato un array di \(n\) interi: \[\text{a}[1], \text{a}[2], \ldots, \text{a}[n]\]
- Ci vengono chieste \(q\) query della forma:
dati \(l\) e \(r\), quanto vale \(\text{a}[l] + \text{a}[l+1] + \cdots + \text{a}[r]\)? - Ci vengono chieste \(u\) query della forma:
dati \(x\) e \(y\), assegnare \(\text{a}[x] = y\).
Fenwick trees
Introduzione
- A differenza di quanto il nome suggerisce, è più facile pensare ai Fenwick tree non come alberi, bensì come array.
- L'idea alla base dei Fenwick tree è trovare un modo efficiente di suddividere l'array iniziale in parti, sfruttando l'ipotesi di IFU.
- Dato un array lungo \(n\), la scomposizione alla base dei Fenwick tree è tale che vengono individuate \(n\) parti e che ogni prefisso è unione di \(\mathcal{O}(\log n)\) parti.
- Allo stesso modo, come vedremo, nell'aggiornare un valore dell'array si rende necessario aggiornare \(\mathcal{O}(\log n)\) parti.
- Assumendo che l'unione di due parti e l'aggiornamento di una singola parte siano operazioni eseguibili in tempo costante, si deduce che ogni query e ogni update costa \(\mathcal{O}(\log n)\) tempo.
- L'implementazione di un Fenwick tree è molto semplice: richiede circa 15 righe di codice.
Fenwick trees
La struttura generale
Dato l'array \(\text{a}\) di dimensione \(n\), il Fenwick Tree associato ad \(\text{a}\), per l'operazione di somma, è un secondo array \(\text{ft}\) di dimensione \(n\), in cui vale che \[\text{ft}[k] = \text{a}[\bar{k}+1] + \cdots + \text{a}[k]\] dove \(\bar{k} = k - \text{lsb}(k)\) è il valore di \(k\) privato del suo bit meno significativo (lsb, least significant bit).
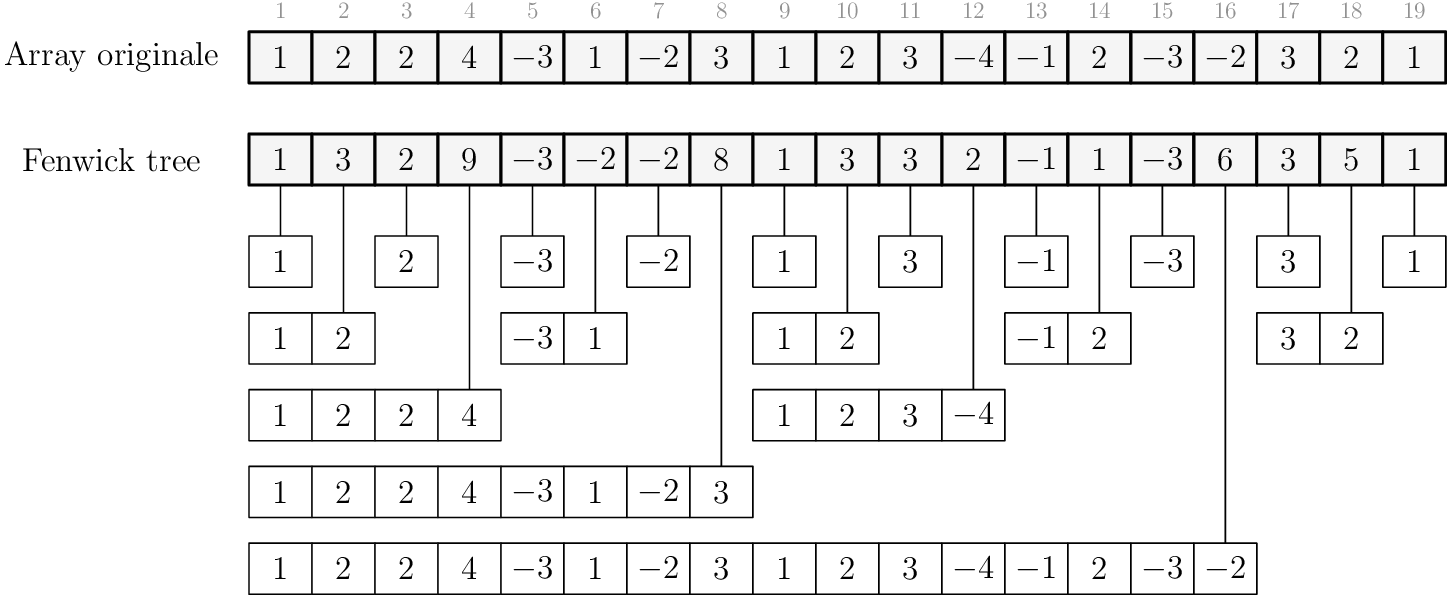
Fenwick trees
Somma di un prefisso
È facile determinare la somma del prefisso \(\text{a}[1..k]\) in tempo \(\mathcal{O}(\log(k)) = \mathcal{O}(\log(n))\). Nell'esempio sotto \(k\) vale \(13\):
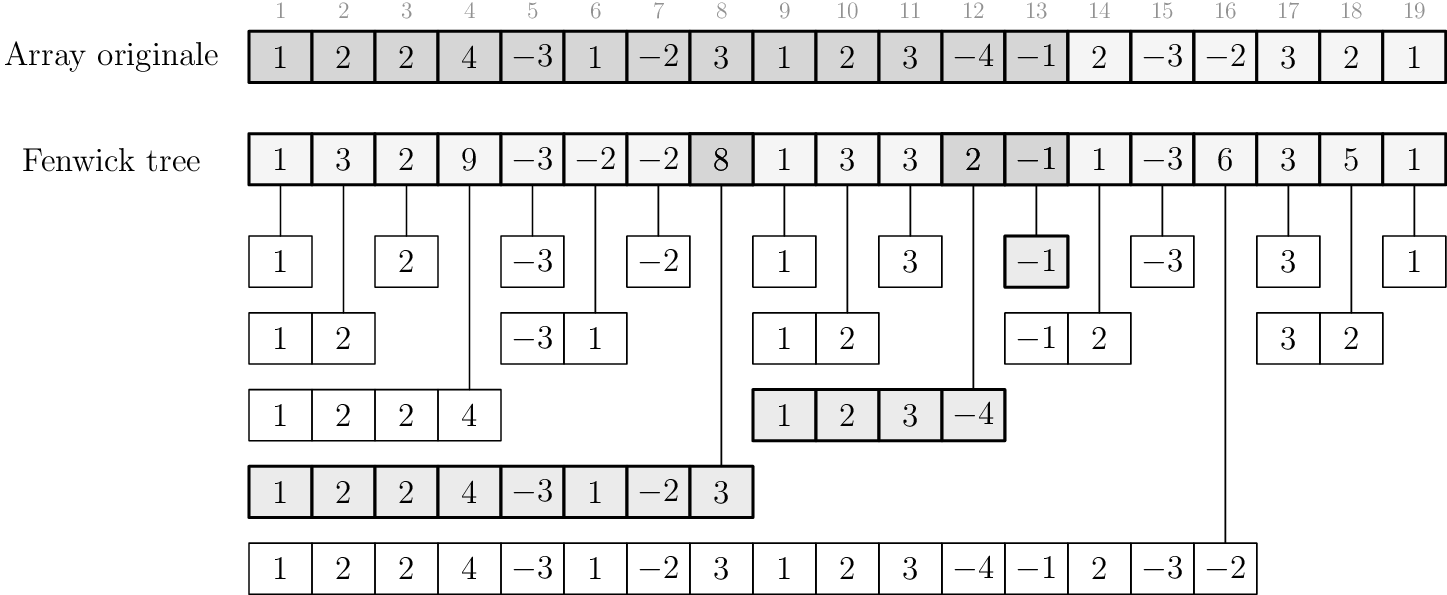
| Da (escluso) | A (incluso) | Somma |
|---|---|---|
| \(12 = \text{01100}_2\) | \(13 = \text{01101}_2\) | \(-1\) |
| \(8 = \text{01000}_2\) | \(12 = \text{01100}_2\) | \(2\) |
| \(0 = \text{00000}_2\) | \(8 = \text{01000}_2\) | \(8\) |
Il numero di valori da sommare è pari al numero di bit settati di \(k\), e quindi \(\mathcal{O}(\log k)\).
Fenwick trees
Somma di un prefisso
#define lsb(x) (x & (-x))
...
struct ft_t {
...
// Calcola la somma del prefisso [1, k]
int sum(size_t k) const {
int ans = 0;
for (; k != 0; k -= lsb(k))
ans += ft[k];
return ans;
}
// Calcola la somma del sottoarray [a, b]
int sum(size_t a, size_t b) const {
return sum(b) - sum(a - 1);
}
...
};
Fenwick trees
Modifica di un valore
Supponiamo di aver modificato il valore in posizione \(x\) dell'array, aggiungengogli una quantità \(\delta\), positiva o negativa. Per semplicità riferiamoci all'esempio qui sotto, avendo posto \(x = 5, \delta=4\).

Fenwick trees
Modifica di un valore
Supponiamo di aver modificato il valore in posizione \(x\) dell'array, aggiungengogli una quantità \(\delta\), positiva o negativa. Per semplicità riferiamoci all'esempio qui sotto, avendo posto \(x = 5, \delta=4\).
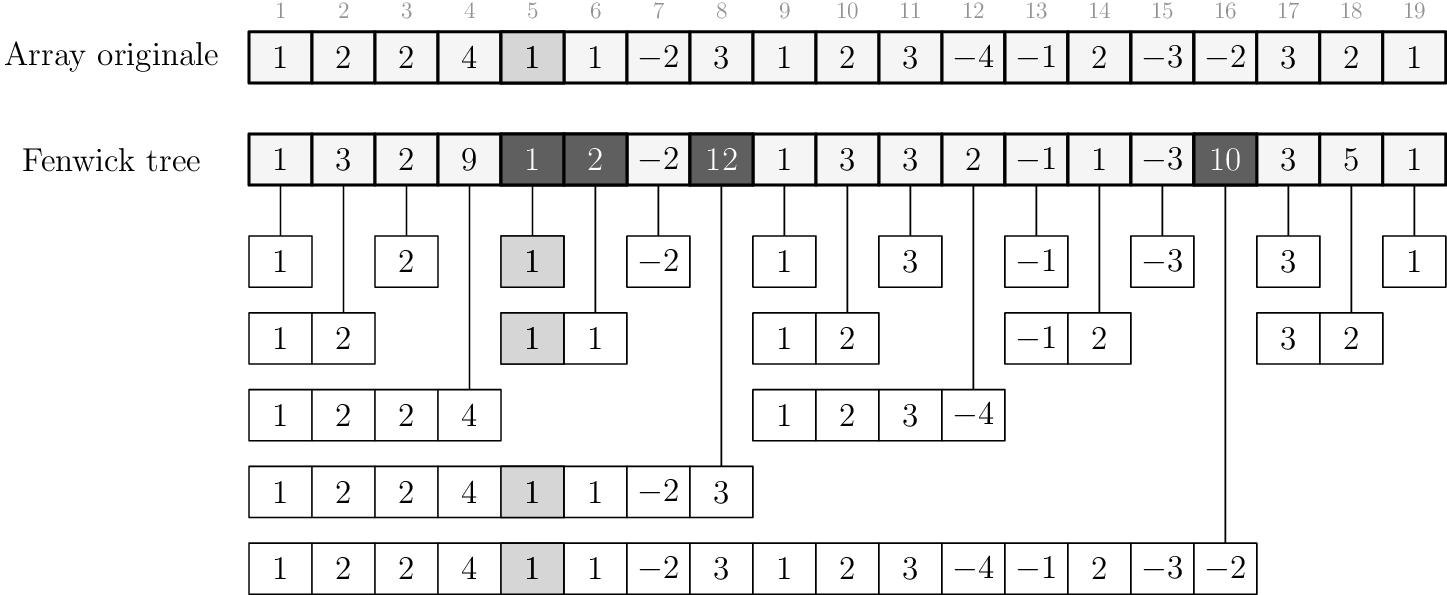
Fenwick trees
Modifica di un valore
Nell'esempio precedente abbiamo visto che la modifica \(\text{a}[5] = \text{a}[5] + 4\) si riflette sul Fenwick tree così:
- \(\text{ft}[5] = \text{ft}[5] + 4\)
- \(\text{ft}[6] = \text{ft}[6] + 4\)
- \(\text{ft}[8] = \text{ft}[8] + 4\)
- \(\text{ft}[16] = \text{ft}[16] + 4\)
Nel caso generale \(\text{a}[x] = \text{a}[x] + \delta\) si può dimostrare (è facile ma un po' noioso e non aggiunge valore al ragionamento) che le posizioni da aggiornare sono:
- \(i_1 = x\) \(\rightarrow\quad\text{ft}[i_1] = \text{ft}[i_1] + \delta\)
- \(i_2 = i_1 + \text{lsb}(i_1)\) \(\rightarrow\quad\text{ft}[i_2] = \text{ft}[i_2] + \delta\)
- \(i_3 = i_2 + \text{lsb}(i_2)\) \(\rightarrow\quad\text{ft}[i_3] = \text{ft}[i_3] + \delta\)
- ...
- finchè la posizione appartiene all'array, cioè è \(\le n\).
Fenwick trees
Modifica di un valore
Il codice corrispondente è particolarmente semplice, e si riduce a un paio di righe:
#define lsb(x) (x & (-x))
...
struct ft_t {
...
// Aggiungi delta alla posizione k
void update(size_t k, int delta) {
for (; k <= n; k += lsb(k))
ft[k] += delta;
}
...
};
Attenzione: la struttura è 1-based, chiamare update(0, x) causa un loop infinito!
Fenwick trees
Alcuni commenti
Il Fenwick tree si estende in modo naturale quando, invece della somma, si è interessati ad altre operazioni associative e invertibili. L'invertibilità è un tassello fondamentale per poter ottenere informazioni su sottoarray che non sono prefissi o suffissi in tempo logaritmico nella dimensione dell'array.
È bene ricordare che in certe applicazioni tuttavia si è interessati sempre solo ai prefissi (o ai suffissi), e quindi che i Fenwick tree sono una opzione da tenere in considerazione (vedremo un esempio in cui useremo la funzione \(\max\) nei prefissi).
Non è necessario scrivere codice ad-hoc per inizializzare un Fenwick tree a partire da un vettore già riempito: per creare il Fenwick tree corrispondente basta chiamare ripetutamente la funzione update per inserire uno ad uno i valori del vettore nel Fenwick tree.
Fenwick trees
Alcuni commenti
Per come abbiamo costruito la struttura, questa deve essere 1-based. Tuttavia, può essere comodo, ad esempio per motivi di consistenza del codice, che i metodi della struttura siano riadattati per accettare posizioni 0-based:
struct ft_t {
int n;
vector<int> ft;
// Costruttore
ft_t(size_t n): n(n), ft(n+1) {}
// Aggiungi delta alla posizione k
void update(size_t k, int delta) {
for (++k; k <= n; k += lsb(k))
ft[k] += delta;
}
// Calcola la somma del prefisso [0, k]
int sum(size_t k) const {
int ans = 0;
for (++k; k != 0; k -= lsb(k))
ans += ft[k];
return ans;
}
// Calcola la somma del sottoarray [a, b]
int sum(size_t a, size_t b) const {
return sum(b) - sum(a - 1);
}
};
Numero di inversioni
Problema classico
Data una permutazione \(\text{a}\) dei numeri da \(1\) a \(n\), una inversione è una coppia \((i,j)\) di indici tale che \[i < j \quad\land\quad \text{a}[i] > \text{a}[j]\]
Data la permutazione, contare le inversioni in tempo \(\mathcal{O}(n \log n)\).
Numero di inversioni
Soluzione
L'idea di fissare un estremo e provare a vedere quanto velocemente si è in grado di determinare le posizioni possibili per l'altro estremo è una idea estremamente generale e ricorrente.
In questo caso scegliamo di fissare \(j\) (il caso con \(i\) è esattamente simmetrico): siamo ora interessati a contare per quanti \(i < j\) accade che \(\text{a}[i] > \text{a}[j]\).
Notiamo che una volta fissato il valore \(j\) anche il valore di \(\text{a}[j]\) è fissato. In altre parole, fissato \(j\), il problema si riduce a determinare, all'interno del suffisso \(\text{a}[1..j-1]\), quanti sono i valori inferiori ad \(\text{a}[j]\).
Supponiamo di possedere una struttura dati in grado di supportare queste operazioni:
- aggiungi un numero (nel range \([1, n]\)) alla collezione
- conta quanti numeri sono maggiori di \(x\)
Spesso è necessario calcolare una quantità per ogni suffisso si può ragionare in questo modo.
Numero di inversioni
Soluzione
Avremmo in quel caso risolto il problema:
int inversioni = 0;
for (int j = 0; j < n; j++) {
inversioni += struttura.quanti_maggiori(a[j]);
struttura.aggiungi_numero(a[j]);
}
return inversioni;
La struttura contiene ad ogni passaggio i numeri nel suffisso, e sa determinare l'informazione necessaria. La struttura in realtà non è nient'atro che un Fenwick tree. Consideriamo infatti un array \(\text{count}\), dove \(\text{count}[i]\) contiene quanti numeri di valore \(i\) sono stati inseriti
- aggiungi_numero(\(x\)) semplicemente si riduce a \(\text{count}[x] = \text{count}[x] + 1\);
- quanti_maggiori(\(x\)) si riduce a domandare la somma del suffisso \((x,n]\).
Longest Increasing Subsequence (LIS)
Problema classico
Dato un array \(\text{a}\) di \(n\) valori nel range \([1,n]\), trovare la lunghezza della sottosequenza crescente più lunga.
Dato l'array, trovare la risposta in \(\mathcal{O}(n \log n)\).
Longest Increasing Subsequence
Soluzione
Come prima, fissiamo un estremo: in questo caso fissato \(j\) siamo interessati a conoscere la lunghezza di una LIS che termina con \(\text{a}[j]\).
Sappiamo che \[\text{lis}(j) = 1 + \max_{i < j\ \land\ \text{a}[i] < \text{a}[j]}\left\{\text{lis}[i]\right\}\] (nel caso in cui non esista nessun \(i\) che rispetti la condizione, quel massimo vale 0).
Come prima, notiamo che il massimo riguarda un determinato prefisso. Sembra sensato quindi provare a costruire induttivamente la risposta.
Come prima, siamo riusciti ad eliminare la condizione \(i < j\) dal massimo. Dobbiamo ancora capire come determinare velocemente \[\max_{\text{a}[i] < \text{a}[j]}\left\{\text{lis}[i]\right\}.\]
Longest Increasing Subsequence
Soluzione
Più astrattamente, possiamo interpretare questo sottoproblema come la costruzione di un dizionario che supporti:
- Inserire una coppia (chiave, valore)
- Restituire il massimo dei valori aventi chiave minore di \(x\)
Il problema in effetti è semplicemente una versione più avanzata di quanto accadeva nel caso delle inversioni, in cui chiave e valore coincidevano. Non dobbiamo dimenticare che anche in questo caso le chiavi appartengono all'intervallo \([1,n]\).
int lis = 0;
for (int j = 0; j < n; j++) {
int lunghezza = 1 + struttura.max_chiavi_minori(a[j]);
struttura.inserisci(a[j], lunghezza);
}
return lis;
Longest Increasing Subsequence
Soluzione
La struttura dati si ottiene considerando un Fenwick tree costruito rispetto alla funzione massimo:
- L'inserimento è esattamente l'operazione di update del Fenwick tree: update(chiave, valore);
- Il massimo corrisponde al metodo che prima avevamo chiamato sum.
struct max_ft_t {
// Il costruttore inizializza tutto a 0 inizialmente
...
// array[k] = max(array[k], val)
void inserisci(size_t chiave, int valore) {
for (; chiave <= n; chiave += lsb(chiave))
ft[chiave] = max(ft[chiave], valore);
}
// Calcola il max del prefisso [1, k]
int max_chiavi_minori(size_t chiave) const {
int ans = 0;
for (; chiave != 0; chiave -= lsb(chiave))
ans = max(ans, ft[chiave]);
return ans;
}
};
Fenwick trees
Range updates, point queries
Esiste un "trucchetto" che è bene conoscere, in quanto viene comodo meno raramente di quanto possa sembrare.
Supponiamo di dover risolvere il problema:
- Ci viene dato un array di \(n\) interi: \[\text{a}[1], \text{a}[2], \ldots, \text{a}[n]\]
- Ci vengono chieste \(q\) query della forma:
dato \(x\), quanto vale \(\text{a}[x]\)? - Ci vengono chieste \(u\) query della forma:
dati \(l, r, \delta\), assegnare \(\text{a}[l] = \text{a}[l] + \delta, \ldots, \text{a}[r] = \text{a}[r] + \delta\).
Fenwick trees
Range updates, point queries
I Fenwick tree supportano entrambe le operazioni in tempo \(\mathcal{O}(\log n)\). La chiave di volta risiede non nel mantenere \(\text{a}\), bensì nel mantenere la sua "derivata discreta", ovvero il vettore \(\text{diff}\) delle differenze finite di \(\text{a}\):

Questa rappresentazione ha la proprietà che \[\text{a}[k] = \text{diff}[1] + \cdots + \text{diff}[k]\quad k = 1, \ldots, n\]
Inoltre, aggiungere una quantità \(\delta\) a \(\text{a}[l], \ldots, \text{a}[r]\) si traduce su \(\text{diff}\) nelle due operazioni elementari:
- \(\text{diff}[l] = \text{diff}[l] + \delta\)
- \(\text{diff}[r+1] = \text{diff}[r+1] - \delta\), se \(r+1 \le n\)
Fenwick trees
Range updates, point queries
Consideriamo a titolo di esempio l'aggiornamento nell'immagine, dove si è posto \(l = 6, r = 12, \delta = 1\):


È quindi sufficiente costruire il Fenwick tree associato a \(\text{diff}\) e mantenere quello.
Pláce
Problema (COCI 3/2011)
Viene dato un organigramma aziendale (un albero) con \(n\) posizioni. Per ogni persona ci viene detto il salario percepito.
Vegono fatte \(q\) richieste della forma:
- 1) Dati \(i\) e \(\delta\), aumenta il salario di tutte le persone agli ordini di \(i\) (cioè tutto il sottoalbero radicato in \(i\)) di una quantità \(\delta\).
- 2) Dato \(i\), stampa il salario percepito in questo momento dalla persona \(i\).
Fenwick trees
Note finali
- È possibile modificare i Fenwick tree in modo che risolvano anche il caso di modifiche su range e domande di somme su prefissi.
- Tuttavia la modifica è poco intuitiva e non rappresenta una alternativa efficace rispetto alla struttura dati più potente/versatile che introdurremo tra poco (i range tree statici).
I Fenwick tree sono strutture interessanti perchè:
- Implementazione brevissima
- Usano poca memoria
- Query e update in tempo logaritmico
Tuttavia hanno delle limitazioni:
- Spesso non sono indicati per query su sottoarray nel caso generale di IFU (funzionano bene solo prefissi/suffissi).
- Range query + range update non banale
3 — Sparse tables
Sparse tables
Introduzione
Prima di arrivare alla seconda struttura dati importante dopo i Fenwick tree della lezione, consideriamo una categoria speciale di IFU che non sono invertibili (e quindi non possono essere maneggiate efficacemente dai Fenwick tree): le IFU idempotenti.
Si tratta di tutte quelle informazioni tali che possono essere ricostruite anche a partire da suddivisioni in parti con intersezione non nulla. Alcuni esempi sono:
- \(\min, \max\)
- \(\gcd\)
In particolare, il problema di trovare il minimo in sottoarray di un array statico è un problema particolarmente studiato data la sua connessione al problema del minimo antenato comune negli alberi.
Le sparse tables sono strutture dati molto semplici in grado di risolvere il problema statico (quindi senza aggiornamento dei valori) di trovare l'informazione idempotente richiesta in tempo costante a valle di un preprocessing tendenzialmente \(\mathcal{O}(n \log n)\), con \(n\) la dimensione dell'array di partenza.
Sparse tables
La struttura
Siano \(\text{a}[1], \ldots, \text{a}[n]\) gli \(n\) valori dell'array. La sparse table associata a questi è una matrice.
Supponiamo di dover calcolare il minimo. Alla riga \(h\), in posizione \(x\) è memorizzata la quantità \[\min\{\text{a}[x], \text{a}[x + 1], \ldots, \text{a}[x + 2^h - 1]\}.\]
Per \(h = 0\) la riga della matrice coincide con l'array originale.
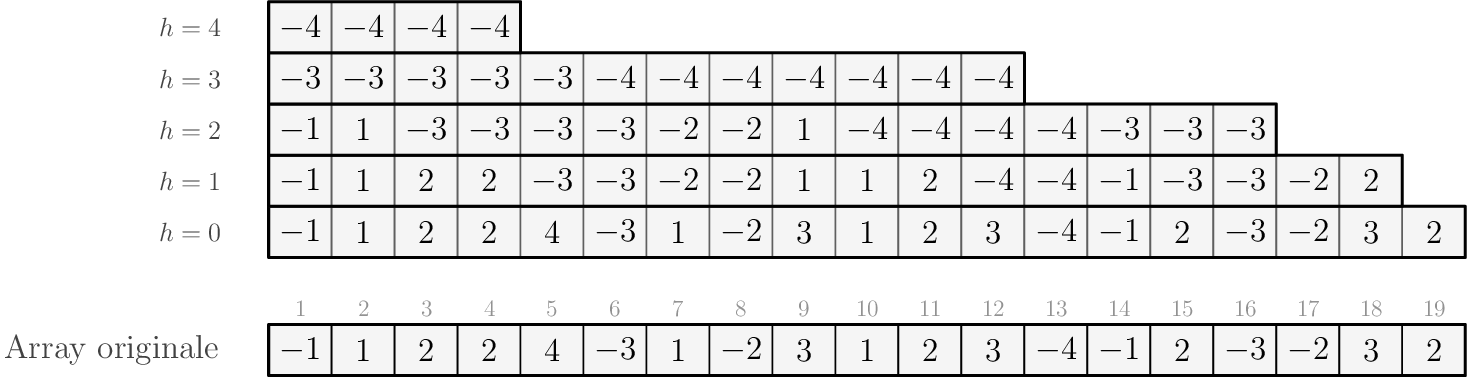
Il numero di posizioni sensate sono circa \(n \log n\): \(\log n\) righe da circa \(n\) valori ognuna.
Sparse tables
Inizializzazione
Costruire una sparse table è particolarmente semplice:
- La riga \(0\) coincide con l'array originale
- Per le righe oltre la \(0\) vale la relazione \[\text{sparse}[h][x] = \min\{\text{sparse}[h-1][x],\text{sparse}[h-1][x + 2^{h-1}]\}.\]
void init(int a[]) {
// Copia l'array originale nella riga 0 della sparse table
for (int i = 0; i < n; i++) {
sparse[0][i] = a[i];
}
// Costruisci tutte le altre righe
for (int h = 1; (1 << h) <= n; h++) {
for (int i = 0; i < n - (1 << h) + 1; i++) {
sparse[h][i] = min(sparse[h - 1][i], sparse[h - 1][i + (1 << (h-1))]);
}
}
}
Sparse tables
Query
Per trovare in tempo logaritmico il minimo degli elementi dalla posizione \(l\) alla posizione \(r\) inclusa, operiamo così:
- Troviamo il più grande \(h\) tale che \[2^h \le r - l + 1.\]
- La risposta alla query è \[\min\{\text{sparse}[h][l],\text{sparse}[h][r - 2^{h} + 1]\}.\]
int query(int l, int r) {
// Trova il valore di h
int h = 0;
for (; (1 << h) <= r - l + 1; h++);
return min(sparse[h][l], sparse[h][r - (1 << h) + 1]);
}
Per risparmiare il fattore logaritmico associato alla ricerca del valore di \(h\), possiamo precalcolare per ogni possibile valore di \(r - l + 1\) il valore di \(h\) associato.
4 — Range trees
Range trees
Problema
Ancora una volta cominciamo da un problema:
- Ci viene dato un array di \(n\) interi: \[\text{a}[1], \text{a}[2], \ldots, \text{a}[n]\]
- Ci vengono chieste \(q\) query della forma:
dati \(l\) e \(r\), quanto vale \(\min\{\text{a}[l], \text{a}[l+1], \ldots, \text{a}[r]\}\)? - Ci vengono chieste \(u\) updates della forma:
dati \(x\) e \(y\), assegnare \(\text{a}[x] = y\).
Range trees
Introduzione
Concettualmente i range tree non aggiungono nulla di nuovo ai Fenwick tree:
- Effettuano una scomposizione di un array di lunghezza \(n\) in \(\mathcal{O}(n)\) parti
- Ogni sottoarray (non più quindi solo i prefissi) può essere ricostruito a partire da \(\mathcal{O}(\log n)\) parti
- Ogni volta che si aggiorna un valore si rende necessario aggiornare \(\mathcal{O}(\log n)\) parti
La struttura interna è però parecchio diversa: i range tree sono alberi veri e propri
I range tree sono alberi binari di ricerca bilanciati (BBST), ma statici (sono i "fratelli minori" e depotenziati di strutture dati molto potenti). Come tali, riescono a svolgere tutti i compiti dei fenwick tree, ma sono un po' più lunghi da implementare, e leggermente più lenti nella pratica.
Tendenzialmente, nei casi in cui i Fenwick tree riescono a risolvere il compito in modo efficiente, questi sono preferibili ai range tree. Per molti problemi tuttavia i Fenwick tree non sono abbastanza potenti, ed è necessario utilizzare strutture più sofisticate, come i range tree.
Range trees
Struttura
Un range tree viene sempre costruito su un numero di foglie che è una potenza di 2. Se l'array di partenza non è lungo quanto una potenza di 2, è sempre possibile "allungarlo", fino a farlo diventare lungo quanto una potenza di due.
La radice corrisponde al nodo 1. Inoltre il figlio sinistro del nodo \(x\) ha indice \(2x\), mentre quello destro \(2x + 1\).
Ogni nodo ha associato un intervallo di competenza, nel modo indicato nella figura:
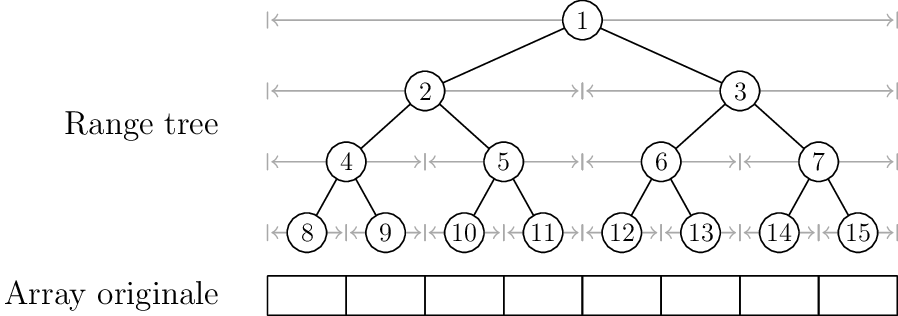
Range trees
Struttura
L'idea, come al solito, è che ogni nodo mantiene l'informazione desiderata riguardo a tutte le posizioni dell'array che ricadono nell'intervallo di competenza
Nel caso del problema che stiamo analizzando, quindi:
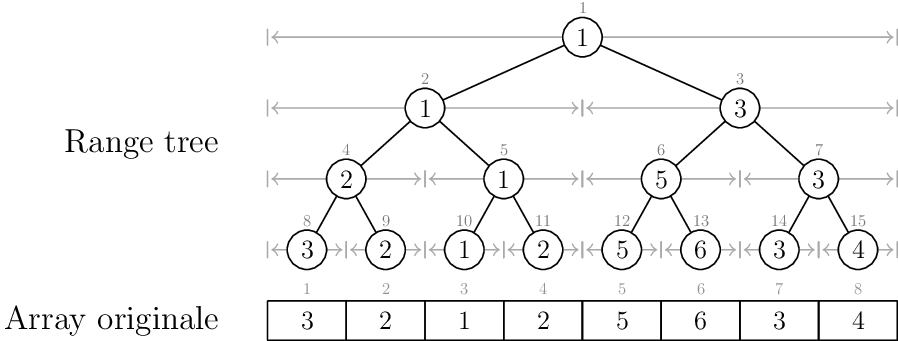
Range trees
Rispondere alle query
Supponiamo di voler determinare l'elemento di valore minimo nel sottoarray [2, 6]
Osserviamo le parti coinvolte:
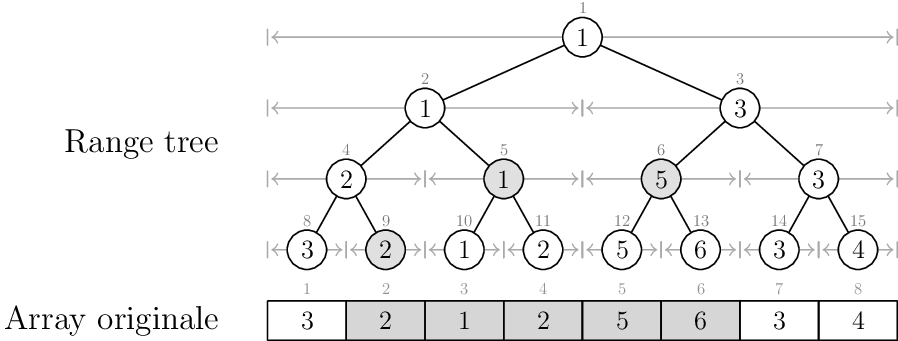
La risposta è \(\min\{2, 1, 5\} = 1\), che in effetti corrisponde al minimo del sottoarray evidenziato.
Range trees
Rispondere alle query
Il codice per trovare i nodi da unire è simile ad una DFS sull'albero. Se \([a,b)\) è il sottoarray su cui si ricerca l'informazione e \([l, r)\) è l'intervallo di competenza del nodo corrente, si pongono 3 casi:
- \([l, r) \subseteq [a, b)\), cioè \(l \ge a \land r \le b\): non è necessario proseguire oltre, questo nodo contiene tutte le informazioni che servono, e le "uniamo" alla risposta finale.
- \([l, r) \cap [a,b) = \varnothing\), cioè \(l \ge b \lor r \le a\): questo nodo (e tutto il suo sottoalbero) non contengono informazioni riguardo al sottoarray in considerazione, quindi non è necessario proseguire.
- \([l, r)\) ha intersezione non nulla con \([a, b)\), ma non è contenuto in esso. In questo caso è necessario proseguire nella visita e ricorrere sui figli del nodo corrente.
La funzione query ha quindi prototipo:
query(id, l, r, a, b)
Range trees
Rispondere alle query
int get_min(const int id, const int l, const int r, const int a, const int b) {
if (r <= a || l >= b) // Completamente fuori
return INFTY;
if (l >= a && r <= b) // Completamente dentro
return tree[id].min;
//else
int mid = (l + r) / 2;
return std::min(
get_min(2 * id, l, mid, a, b),
get_min(2 * id + 1, mid, r, a, b)
);
}
Range trees
Modifica di un valore
Supponiamo di aver modificato il valore in posizione \(x\) dell'array, sostituendolo col valore \(y\). Per semplicità riferiamoci all'esempio qui sotto, avendo posto \(x = 6, y=4\).

Range trees
Modifica di un valore
Supponiamo di aver modificato il valore in posizione \(x\) dell'array, sostituendolo col valore \(y\). Per semplicità riferiamoci all'esempio qui sotto, avendo posto \(x = 6, y=4\).
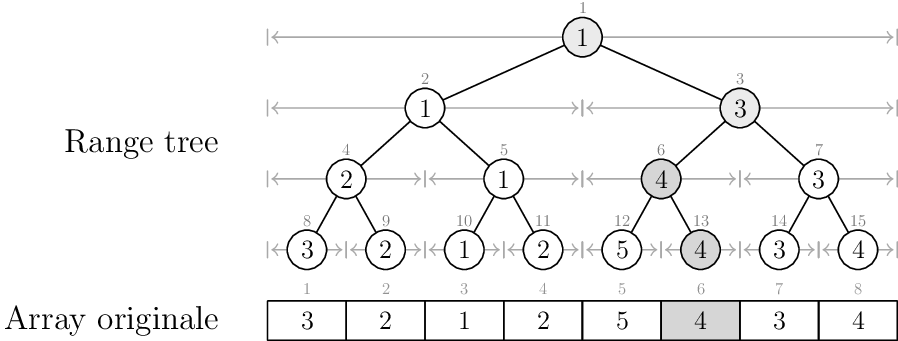
Range trees
Modifica di un valore
Il codice top-down per la modifica di un valore è semplice:
void update(const int id, const int l, const int r, const int x, const int y) {
if (r <= x || l >= x + 1)
return;
if (r > l + 1) { // non sono una foglia
int mid = (l + r) / 2;
update(2 * i, l, mid, x, y);
update(2 * i + 1, mid, r, x, y);
tree[id].min = std::min(
tree[2 * id].min,
tree[2 * id + 1].min
);
}
else { // sono una foglia
tree[id].min = y;
}
}
Range trees
Modifica di un sottoarray
Supponiamo di voler ora aggiornare un intero sottoarray, ad esempio settando il valore di ogni cella in \([a,b)\)ad un certo intero \(y\).
Con riferimento all'esempio che stiamo portando avanti, supponiamo di voler impostare a 3 tutto il subarray \([2, 7)\)
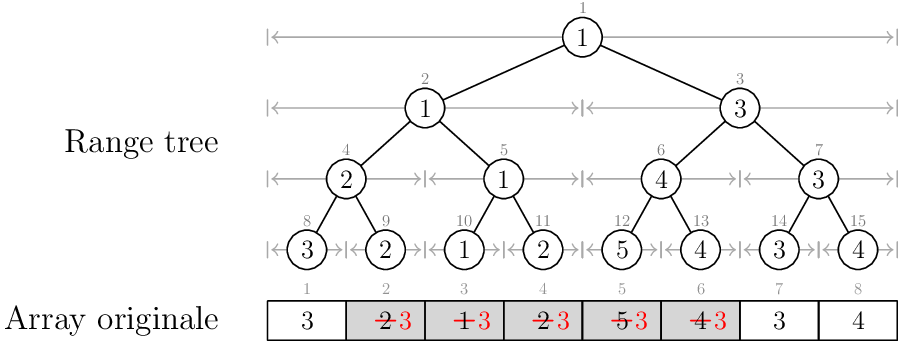
Range trees
Modifica di un sottoarray
L'idea questa volta è di tenere in ogni nodo l'informazione se è necessario eseguire una certa operazione su tutte le radici del suo sottoalbero. Ad esempio, ogni nodo del range tree dell'esempio sa se le sue foglie sono da settare ad un valore fissato, e in caso quale valore.
L'invariante che vogliamo mantenere in ogni istante è che:
- Tutti i discendenti di un nodo che deve ancora aggiornare le sue foglie contengono informazioni potenzialmente vecchie
- Tutti gli antenati del nodo che deve ancora aggiornare le sue foglie contengono informazioni corrette
Per quanto riguarda questo esempio, possiamo immaginare che ogni nodo mantenga, oltre a \(\text{min}\), anche \(\text{set_value}\), il valore da impostare alle foglie, e \(\text{modified}\), se il nodo deve ancora propagare l'informazione ai figli.
Range trees
Modifica di un sottoarray
Ritornando all'esempio di prima:
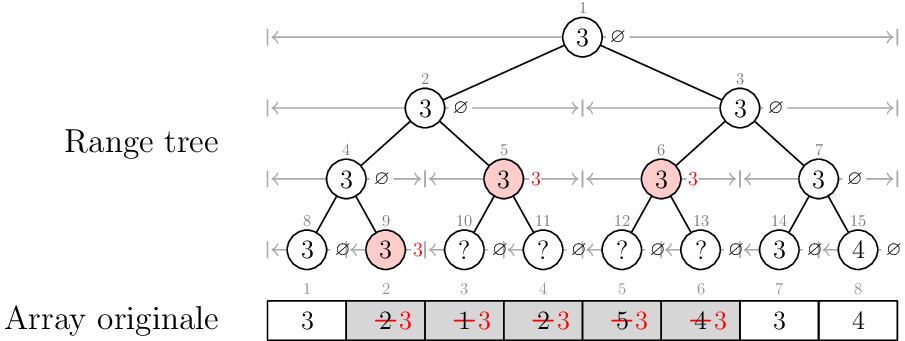
Range trees
Modifica di un sottoarray
int get_min(const int id, const int l, const int r, const int a, const int b) {
if (r <= a || l >= b) // Completamente fuori
return INFTY;
if (l >= a && r <= b) // Completamente dentro
return tree[id].min;
if (node[id].modified) // Nota: il nodo non può essere una foglia (perchè?)
propagate(id);
//else
int mid = (l + r) / 2;
return std::min(
get_min(2 * id, l, mid, a, b),
get_min(2 * id + 1, mid, r, a, b)
);
}
Range trees
Modifica di un sottoarray
void update(const int id, const int l, const int r, const int a, const int b, const int y) {
if (r <= a || l >= b) // Completamente fuori
return;
if (l >= a && r <= b) { // Completamente dentro
tree[id].set_value = min(tree[id].set_value, y);
tree[id].min = tree[id].set_value;
tree[id].modified = true;
return;
}
if (node[id].modified) // Nota: il nodo non può essere una foglia (perchè?)
propagate(id);
int mid = (l + r) / 2;
update(2 * id, l, mid, a, b, y);
update(2 * id + 1, mid, r, a, b, y);
tree[id].min = std::min(
tree[2 * id].min,
tree[2 * id + 1].min
);
}
Range trees
Modifica di un sottoarray
void propagate(const int id) {
// Nota: si assume che il nodo id non sia una foglia
tree[2 * id].set_value = min(tree[id].set_value, tree[2 * id].set_value);
tree[2 * id].min = tree[id].min;
tree[2 * id].modified = true;
tree[2 * id + 1].set_value = min(tree[id].set_value, tree[2 * id + 1].set_value);
tree[2 * id + 1].min = tree[id].min;
tree[2 * id + 1].modified = true;
tree[id].set_value = INFTY;
tree[id].modified = false;
}
</lezione>
