- 1.
-
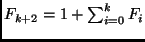 ;
;
- 2.
-
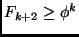 ,
dove
,
dove
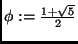 indica la sezione aurea.
indica la sezione aurea.
Svolgimento Esercizio 1
Con riferimento al precedente esercizio,
sapresti dimostrare
che in un qualsiasi momento,
ed ove ![]() sia un qualsiasi nodo di albero
della nostra foresta con, diciamo,
sia un qualsiasi nodo di albero
della nostra foresta con, diciamo, ![]() figli,
allora la cardinalità della discendenza di
figli,
allora la cardinalità della discendenza di ![]() ,
ossia il numero di nodi del sottoalbero radicato in
,
ossia il numero di nodi del sottoalbero radicato in ![]() ,
è almeno
,
è almeno ![]() .
.
Svolgimento Esercizio 2
Si fissi l'attenzione su un qualsiasi istante
della felice storia della nostra famigliola di guardiaboschi.
Si indichi con ![]() la cardinalità della discendenza di
la cardinalità della discendenza di ![]() .
Per induzione su
.
Per induzione su ![]() ,
mostreremo che,
,
mostreremo che,
![]() per un qualsiasi nodo
per un qualsiasi nodo ![]() con
con ![]() figli.
A quel punto il risultato desiderato seguirà come conseguenza
della proprietà di cui al Punto 2 dell'Esercizio 1.
figli.
A quel punto il risultato desiderato seguirà come conseguenza
della proprietà di cui al Punto 2 dell'Esercizio 1.
base: Chiaramente, se ![]() ha
ha ![]() figli,
allora la sua discendenza si compone solamente di
figli,
allora la sua discendenza si compone solamente di ![]() stesso,
ossia
stesso,
ossia ![]() .
Inoltre, se
.
Inoltre, se ![]() ha un figlio,
allora
ha un figlio,
allora
![]() .
.
passo:
Siano
![]() i figli di
i figli di ![]() nell'ordine in cui sono stati innestati in
nell'ordine in cui sono stati innestati in ![]() .
Chiaramente,
.
Chiaramente,
![]() .
Mostreremo innanzittutto che
.
Mostreremo innanzittutto che
![]() per ogni
per ogni ![]() .
Infatti, quando
.
Infatti, quando ![]() è stato innestato in
è stato innestato in ![]() ,
il nodo
,
il nodo ![]() aveva almeno
aveva almeno ![]() figli:
figli:
![]() .
Siccome una radice può venire innestata come
figlia di un'altra radice solamente quando esse hanno lo stesso
numero di figli, allora
.
Siccome una radice può venire innestata come
figlia di un'altra radice solamente quando esse hanno lo stesso
numero di figli, allora ![]() aveva almeno
aveva almeno ![]() figli
quando
figli
quando ![]() è stato innestato in
è stato innestato in ![]() .
Da quel momento
.
Da quel momento ![]() può aver perso al più un solo
figlio, per come è stata definita l'operazione di potatura
e visto che
può aver perso al più un solo
figlio, per come è stata definita l'operazione di potatura
e visto che ![]() non è stato potato via da
non è stato potato via da ![]() posteriormente
all'innesto discusso.
Ne consegue che
posteriormente
all'innesto discusso.
Ne consegue che ![]() ha almeno
ha almeno ![]() figli nell'istante
su cui abbiamo deciso di fissare la nostra attenzione,
e quindi, per ipotesi induttiva,
figli nell'istante
su cui abbiamo deciso di fissare la nostra attenzione,
e quindi, per ipotesi induttiva,
![]() come sopra affermato.
come sopra affermato.
In virtù della proprietà di cui al Punto 1 dell'Esercizio 1 possiamo ora concludere il nostro passo induttivo come segue:
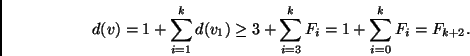
Svolgimento Esercizio 3
Siccome in uno heap di Fibonacci teniamo un puntatore ![]() ad una radice che ospita un elemento a chiave minima
tra le radici (e quindi tra tutti gli elementi ospitati nello heap,
a causa della proprietà dello heap),
non sarà certo difficile restituire un elemento a chiave
minima in
ad una radice che ospita un elemento a chiave minima
tra le radici (e quindi tra tutti gli elementi ospitati nello heap,
a causa della proprietà dello heap),
non sarà certo difficile restituire un elemento a chiave
minima in ![]() .
.
Tuttavia vorremmo non solo individuare ma anche
estrarre dallo heap l'elemento indicatoci da ![]() .
L'estrazione di per se non è difficoltosa in quanto
la lista delle radici è una lista circolare e doubled linked e quindi ho
a disposizione tutte le informazioni necessarie per aprire
il ``braccialetto'' nel punto indicatomi da
.
L'estrazione di per se non è difficoltosa in quanto
la lista delle radici è una lista circolare e doubled linked e quindi ho
a disposizione tutte le informazioni necessarie per aprire
il ``braccialetto'' nel punto indicatomi da ![]() ,
estrarre la perla indirizzata da
,
estrarre la perla indirizzata da ![]() ,
e ricomporre le estremità del ``braccialetto'',
il tutto in
,
e ricomporre le estremità del ``braccialetto'',
il tutto in ![]() .
.
Dove si annida il problema?
Il punto è che non sò più a quale radice dovrà
ora puntare ![]() ,
e di fatto per scoprirlo non posso evitare di scandirmi
l'intera lista delle radici, di lunghezza
,
e di fatto per scoprirlo non posso evitare di scandirmi
l'intera lista delle radici, di lunghezza ![]() ,
impiegando quindi un tempo effettivo di calcolo
,
impiegando quindi un tempo effettivo di calcolo ![]() .
.
Visto allora che questo ![]() lo debbo comunque spendere,
ne approfitto per giocare una Consolidate,
ossia man mano che,
durante la mia scansione della lista redici,
individuo due radici dello stesso grado,
effettuo allora un innesto di una radice nell'altra come
i nostri amici guardiaboschi di cui all'esercizio precedente.
Ovviamente sceglierò quale radice và innestata nell'altra
con l'avvertenza di mantenere la proprità dell'ordinamento dello heap,
cosa che mi è sempre possibile fare in
lo debbo comunque spendere,
ne approfitto per giocare una Consolidate,
ossia man mano che,
durante la mia scansione della lista redici,
individuo due radici dello stesso grado,
effettuo allora un innesto di una radice nell'altra come
i nostri amici guardiaboschi di cui all'esercizio precedente.
Ovviamente sceglierò quale radice và innestata nell'altra
con l'avvertenza di mantenere la proprità dell'ordinamento dello heap,
cosa che mi è sempre possibile fare in ![]() .
Il costo effettivo della Consolidate non sforerà
pertanto sul costo asintotico di
.
Il costo effettivo della Consolidate non sforerà
pertanto sul costo asintotico di ![]() richiesto
per la sola scansione dell'intera lista delle radici,
purchè io abbia l'accortezza di avvalermi di un vettore di appoggio
che mi ricordi, per ogni
richiesto
per la sola scansione dell'intera lista delle radici,
purchè io abbia l'accortezza di avvalermi di un vettore di appoggio
che mi ricordi, per ogni ![]() , se ho lasciato dietro di me nella scansione
una radice con
, se ho lasciato dietro di me nella scansione
una radice con ![]() figli, ed eventualmente il puntatore alla stessa.
figli, ed eventualmente il puntatore alla stessa.
In base a quanto dimostrato nell'Esercizio 2,
siamo garantiti che comunque
![]() ,
e siccome a seguito della Consolidate nel mio giardino
non saranno presenti alberi della stessa varietà (con radici
aventi lo stesso numero di figli),
allora il numero di radici
,
e siccome a seguito della Consolidate nel mio giardino
non saranno presenti alberi della stessa varietà (con radici
aventi lo stesso numero di figli),
allora il numero di radici ![]() a seguito della Consolidate
sarà limitato superiormente da
a seguito della Consolidate
sarà limitato superiormente da ![]() (ossia
(ossia
![]() ).
Durante la consolidate sarà inoltre mia cura di smarcare
quelle radici che vanno ad innestarsi in altre radici,
in modo da mantenere l'invariante che un nodo sia marcato
se e solo se ha subito la perdita di un figlio per potatura
da quando è andato a scegliersi il padre corrente tramite
suo ultimo innesto.
Pertanto, ove si sia indicato con
).
Durante la consolidate sarà inoltre mia cura di smarcare
quelle radici che vanno ad innestarsi in altre radici,
in modo da mantenere l'invariante che un nodo sia marcato
se e solo se ha subito la perdita di un figlio per potatura
da quando è andato a scegliersi il padre corrente tramite
suo ultimo innesto.
Pertanto, ove si sia indicato con ![]() ed
ed ![]() il numero di nodi marcati prima e dopo l'esecuzione della Consolidate,
allora
il numero di nodi marcati prima e dopo l'esecuzione della Consolidate,
allora
![]() .
Ricordiamo che la funzione potenziale scelta
per condurre l'analisi ammortizzata per gli heaps di Fibonacci
ha la seguente forma:
.
Ricordiamo che la funzione potenziale scelta
per condurre l'analisi ammortizzata per gli heaps di Fibonacci
ha la seguente forma:
![]() .
Il costo ammortizzato per l'operazione di EstraiMinimo
sarà pertanto limitato da costo effettivo
meno differenza di potenziale, ossia da
.
Il costo ammortizzato per l'operazione di EstraiMinimo
sarà pertanto limitato da costo effettivo
meno differenza di potenziale, ossia da
L'unità di misura scelta per l'espressione della funzione potenziale è infatti assunta essere tale da dominare ogni altro fattore costante che appare nel costo effettivo di qualsivoglia operazione prevista per gli heaps di Fibonacci. Solitamente, su una qualsiasi struttura dati, viene definito (ed implementato) solamente un numero finito di operazioni, pertanto questa assunzione è sempre legittima e fa parte della prassi nel progetto di una struttura dati nell'ottica dell'analisi ammortizzata.
Svolgimento Esercizio 3
Faremo riferimento (come black-box)
ad uno heap ![]() ed assumeremo implicitamente che la chiave
dell'elemento
ed assumeremo implicitamente che la chiave
dell'elemento ![]() in seno ad
in seno ad ![]() sia il valore di
sia il valore di ![]() .
.
Dimostriamo ora le invarianti proposte:
Svolgimento Esercizio 4
StampaCammino ![]()
Per l'analisi della coplessità dell'algoritmo di Dijkstra
si noti che l'operazione di estrazione di un nodo a ![]() minimo è eseguita al più
minimo è eseguita al più ![]() volte (
volte (![]() se il grafo è
connesso) e quindi possiamo considerare
che il tempo speso in tale operazione sia in tutto
se il grafo è
connesso) e quindi possiamo considerare
che il tempo speso in tale operazione sia in tutto ![]() ,
poichè l'estrazione del minimo prende
,
poichè l'estrazione del minimo prende ![]() sia con gli heaps Binomiali che con quelli di Fibonacci
(ammortizzata).
Parimenti, ogni nodo viene inserito al più una volta
e quindi il tempo complessivo imputabile ad inserimenti
è
sia con gli heaps Binomiali che con quelli di Fibonacci
(ammortizzata).
Parimenti, ogni nodo viene inserito al più una volta
e quindi il tempo complessivo imputabile ad inserimenti
è ![]() .
Si noti che ogni arco può causare al più un solo decremento
di chiave, e precisamente nell'istante in cui il primo dei suoi
estremi diventa nero.
Pertanto, il tempo speso decrementando chiavi
è dominato complessivamente da
.
Si noti che ogni arco può causare al più un solo decremento
di chiave, e precisamente nell'istante in cui il primo dei suoi
estremi diventa nero.
Pertanto, il tempo speso decrementando chiavi
è dominato complessivamente da ![]() ,
dove
,
dove
![]() nel caso degli heaps Binomiali
e
nel caso degli heaps Binomiali
e ![]() nel caso degli heaps di Fibonacci,
ove si faccia riferimento all'analisi ammortizzata.
Il tempo complessivo di calcolo sarà pertanto
limitato da
nel caso degli heaps di Fibonacci,
ove si faccia riferimento all'analisi ammortizzata.
Il tempo complessivo di calcolo sarà pertanto
limitato da
![]() nel caso di implementazione
tramite heaps Binomiali
e da
nel caso di implementazione
tramite heaps Binomiali
e da
![]() nel caso di implementazione
tramite heaps di Fibonacci.
nel caso di implementazione
tramite heaps di Fibonacci.
Svolgimento Esercizio 5
Sia ![]() un vettore di
un vettore di ![]() interi
rappresentati ciascuno da
interi
rappresentati ciascuno da ![]() cifre in base
cifre in base ![]() .
.
RADISORT ![]()
Se l'algoritmo di ordinamento stabile chiamato ogni
volta è il COUNTINGSORT,
allora esso avrà complessità ![]() .
Pertanto la complessità di RADIXSORT
sarà
.
Pertanto la complessità di RADIXSORT
sarà ![]() .
.
L'algoritmo COUNTINGSORT è stabile, ossia in caso di pareggio sulla chiave, viene piazzato prima in output l'elemento che risultava piazzato prima in input. Il RADIXSORT come descritto sopra risulta corretto se l'algoritmo cui fa riferimento è stabile, in quanto possiamo verificare la seguente invariante:
se dei numeri presenti inconsideriamo solo le cifre meno significative, dalla cifra
appena considerata in poi, il vettore
è ordinato.
Controesempio richiesto:
si consideri ![]() .
Dopo averlo ordinato sulla cifra meno significativa otterremo
necessariamente
.
Dopo averlo ordinato sulla cifra meno significativa otterremo
necessariamente ![]() .
Ora però dobbiamo ordinarlo anche sulla cifra più signifivativa.
Se nessuno ci garantisce che l'algoritmo impiegato
per ordinare sulla cifra più significativa sia stabile,
allora non possiamo escludere che l'output sia
.
Ora però dobbiamo ordinarlo anche sulla cifra più signifivativa.
Se nessuno ci garantisce che l'algoritmo impiegato
per ordinare sulla cifra più significativa sia stabile,
allora non possiamo escludere che l'output sia
![]() . Ossia un output errato.
. Ossia un output errato.