Esercizio 1
Sapresti dare uno pseudocodice od una descrizione comunque
efficace e formale per la
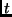 -Selection
-Selection
in tempo lineare?
(La
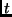 -Selection
-Selection era l'algoritmo
che avevamo proposto per risolvere il
Median Finding Problem
in tempo lineare).
Sapresti esprimere i punti salienti per l'analisi
del running time di tale algoritmo?
Esercizio 2
Per
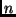
elementi distinti
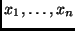
con pesi positivi
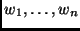
tali che
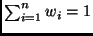
,
il mediano pesato è l'elemento
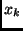
che soddisfa le seguenti diseguaglianze:
e
Fornire un algoritmo che trovi il mediano pesato
in tempo
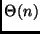
.
Esercizio 3
Agli archi di un grafo
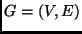
sono associati dei pesi
(valori reali o interi, come preferisci).
Abbiamo cioè una funzione
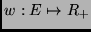
.
Vorremo trovare un albero di copertura
di peso minimo.
Poggiando su uno heap di servizio (preso come black-box),
si dia uno pseudocodice per l'algoritmo
di Prim per il computo di una soluzione ottima.
Si assuma che la soluzione
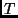
venga costruita a partire
da un certo nodo
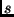
, aggiungendo gli archi uno alla volta.
Nello pseudocodice,
gli archi siano colorati verde, giallo e rosso,
secondo il seguente schema:
- rosso
- ad ogni istante,
è rosso ogni arco che sia
già stato infilato nella soluzione corrente
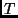 ;
;
- giallo
- si consideri un arco
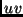 con un estremo
con un estremo 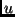 già raggiunto da
già raggiunto da
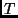 e l'altro estremo
e l'altro estremo 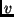 non ancora raggiunto.
L'arco
non ancora raggiunto.
L'arco 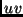 è giallo se
è giallo se 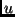 è il primo nodo raggiunto da
è il primo nodo raggiunto da 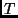 tra quei nodi
tra quei nodi 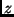 che minimizzano
che minimizzano 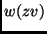 con
con 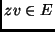 e
e 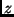 già raggiunto da
già raggiunto da 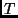 ;
;
- verde
- altrimenti.
Nello pseudocodice,
i nodi siano colorati bianco, grigio e nero,
secondo il seguente schema:
- bianco
- se non si è ancora individuato un cammino
da
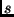 al nodo in questione;
al nodo in questione;
- grigio
- se si è già individuato qualche cammino
da
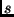 al nodo in questione
al nodo in questione 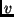 ,
ma
,
ma 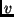 non è stato ancora
estratto dallo heap di servizio;
non è stato ancora
estratto dallo heap di servizio;
- nero
- il nodo in questione è già stato
estratto dallo heap di servizio.
Dimostrare poi le seguenti invarianti:
- 1.
- ad ogni iterazione,
ad uno specifico passo della tua procedura
da te indicato, puoi affermare che i nodi
grigi sono tutti e soli i nodi nello heap di servizio;
- 2.
- quando
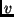 è nero, allora
è nero, allora 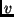 ed
ed 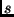 sono già
connessi in seno alla soluzione parziale
sono già
connessi in seno alla soluzione parziale 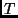 (fatta dagli archi rossi).
(fatta dagli archi rossi).
- 3.
- esiste una soluzione ottima per il
problema ricevuto in input
che contenga
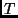 , ossia tutti gli archi rossi.
, ossia tutti gli archi rossi.