- 1.
-
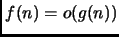 implica
implica
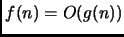 .
.
- 2.
-
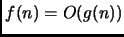 implica
implica
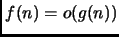 .
.
- 3.
-
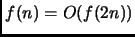 .
.
- 4.
-
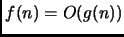 implica
implica
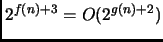 .
.
Svolgimento Esercizio 1
Svolgimento Esercizio 2
Sappiamo che esiste una costante ![]() ed un
ed un ![]() tale che
tale che
![]() Pertanto,
per ogni
Pertanto,
per ogni ![]() ,
,
![]() Ciò dimostra che
Ciò dimostra che
![]() .
.
Svolgimento Esercizio 3
Si noti che, per ogni ![]() ,
,
Riponendo le funzioni proposte secondo tale ordine, abbiamo
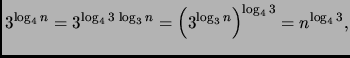 |
|||
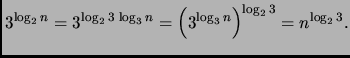 |
Da cui risulta evidente che
Volendo verificarlo ad un più basso livello, abbiamo infatti che
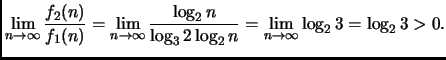
L'unico caso critico è il confronto tra
![]() ed
ed
![]() che non differiscono per una costante moltiplicativa.
La differenza nel loro ordine di crescita
asintotico può essere messa in evidenza utilizzando
il teorema dell'Hôpital, ed osservando che
che non differiscono per una costante moltiplicativa.
La differenza nel loro ordine di crescita
asintotico può essere messa in evidenza utilizzando
il teorema dell'Hôpital, ed osservando che
![]()
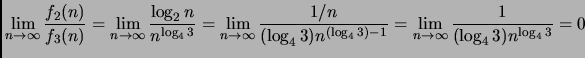
I restanti due casi sono banali, simili al primo, e del tutto analoghi tra di loro. Ne affronteremo pertanto solo uno, e lasciamo l'altro come esercizio mentale.
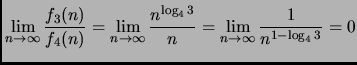
poichè
![]() .
.
Svolgimento Esercizio 4
Avevamo visto a lezione che
![]() .
Come prima cosa,
riconduciamoci pertanto a quanto per noi già noto.
A tal fine, basta una piccola manipolazione algebrica:
.
Come prima cosa,
riconduciamoci pertanto a quanto per noi già noto.
A tal fine, basta una piccola manipolazione algebrica:
Questa era già una risposta parziale all' esercizio,
ma per completarlo, dobbiamo mostrare anche che
![]() .
.
Chiaramente,
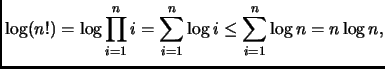
![$\displaystyle \log (n!) = \log \prod_{i=1}^n i = \sum_{i=1}^n \log i
\geq \sum_...
...}^n \log i
\geq \sum_{i=\lceil n/2 \rceil}^n [(\log n) -1]
= \Omega(n\log n),
$](img52.png)
si consideri la seguente procedura iterativa.
#include<iostream.h>
int main() {
int n; cout << "Dammi n: "; cin >> n; cout << endl;
long long int T[n +1]; T[0] = 1;
cout << "T[0] = " << T[0] << endl;
for(int k=1; k<=n; k++) {
T[k] = T[k-1]+T[k-1];
cout << "T[" << n << "] = " << T[n] << endl;
}
}
Si stabilisca l'ordine di crescita del tempo di calcolo della procedura proposta. Si stabilisca l'ordine di crescita della memoria impiegata dalla procedura proposta.
Svolgimento Esercizio 5
La memoria occupata è sicuramente ![]() ,
causa l'allocazione long long int T[n +1]
alla seconda linea del codice proposto.
Infatti, tale linea viene eseguita incondizionatamente,
ad ogni immissione di un input corretto.
,
causa l'allocazione long long int T[n +1]
alla seconda linea del codice proposto.
Infatti, tale linea viene eseguita incondizionatamente,
ad ogni immissione di un input corretto.
La memoria occupata è di fatto ![]() ,
poichè se andiamo a considerare le altre allocazioni di memoria
esplicitamente od implicitamente comportate dal nostro codice,
risulta evidente che, per ogni realizzazione ragionevole di un compilatore,
esse saranno in numero costante
,
poichè se andiamo a considerare le altre allocazioni di memoria
esplicitamente od implicitamente comportate dal nostro codice,
risulta evidente che, per ogni realizzazione ragionevole di un compilatore,
esse saranno in numero costante ![]() , e non dipenderanno cioè
dal valore
, e non dipenderanno cioè
dal valore ![]() in input.
in input.
Il tempo di calcolo impiegato è sicuramente ![]() ,
causa il ciclo for(int k=1; k<=n; k++)
presente alla quarta linea del codice proposto.
Infatti tale ciclo for viene eseguito incondizionatamente, e per intero,
ad ogni immissione di un input corretto.
,
causa il ciclo for(int k=1; k<=n; k++)
presente alla quarta linea del codice proposto.
Infatti tale ciclo for viene eseguito incondizionatamente, e per intero,
ad ogni immissione di un input corretto.
Il tempo di calcolo impiegato è di fatto ![]() ,
poichè le istruzioni contenute
nel ciclo for(int k=1; k<=n; k++)
sono eseguite
,
poichè le istruzioni contenute
nel ciclo for(int k=1; k<=n; k++)
sono eseguite ![]() volte,
mentre quelle esterne al ciclo sono eseguite
volte,
mentre quelle esterne al ciclo sono eseguite ![]() volta.
Inoltre, tutte le istruzioni, è ragionevole aspettarsi,
richiedano
volta.
Inoltre, tutte le istruzioni, è ragionevole aspettarsi,
richiedano ![]() .
A dire il vero, per l'istruzione,
long long int T[n +1],
uno potrebbe chiedersi se essa non possa richiedere più di
.
A dire il vero, per l'istruzione,
long long int T[n +1],
uno potrebbe chiedersi se essa non possa richiedere più di ![]() tempo.
Tuttavia, è ragionevole ipotizzare quantomeno che
il tempo richiesto da tale istruzione sia
tempo.
Tuttavia, è ragionevole ipotizzare quantomeno che
il tempo richiesto da tale istruzione sia ![]() ,
e si noti che tale istruzione è esterna al ciclo for
ed è pertanto eseguita un'unica volta.
,
e si noti che tale istruzione è esterna al ciclo for
ed è pertanto eseguita un'unica volta.
#include<iostream.h>
long long int T(int n) {
if(n==0) return 1;
return T(n-1) + T(n-1);
}
int main() {
int n; cout << "Dammi n: "; cin >> n; cout << endl;
cout << "T[" << n << "] = " << T(n) << endl;
}
Si stabilisca l'ordine asintotico di crescita per il tempo di calcolo della procedura proposta dal professor Tortoise. Si stabilisca l'ordine di crescita della memoria impiegata dalla procedura di Tortoise.
Svolgimento Esercizio 6
Per il tempo di calcolo, possiamo scrivere la seguente ricorrenza,
Ovviamente,
![]() .
Possiamo infatti verificare per sostituzione sia che
.
Possiamo infatti verificare per sostituzione sia che
![]() :
:
sia che
![]() :
:
La contraddizione
![]() è solo apparente ed è dovuta al fatto
che abbiamo lavorato prescindendo dalla base dell'induzione.
è solo apparente ed è dovuta al fatto
che abbiamo lavorato prescindendo dalla base dell'induzione.
Per quanto riguarda l'occupazione di memoria dobbiamo prestare
attenzione al fatto che ad ogni chiamata di procedura
viene allocata una certa quantità di memoria.
Nel caso della nostra semplice procedura
long long int T(int n), tale quantità di memoria risulta essere ![]() .
Quando la procedura termina, tale quantità di memoria viene però rilasciata.
E tuttavia singole quantità di memoria allocate
a fronte di chiamate diverse vengono a sommarsi se la seconda chiamata
avviene prima che la prima chiamata sia già stata esaurita.
Siamo cioè chiamati a valutare l'altezza dell'albero di ricorsione,
che corrispende al massimo numero di ambienti che dovranno essere mantenuti aperti
contemporaneamente.
Nel nostro caso, l'altezza dell'albero di ricorsione risulta essere
.
Quando la procedura termina, tale quantità di memoria viene però rilasciata.
E tuttavia singole quantità di memoria allocate
a fronte di chiamate diverse vengono a sommarsi se la seconda chiamata
avviene prima che la prima chiamata sia già stata esaurita.
Siamo cioè chiamati a valutare l'altezza dell'albero di ricorsione,
che corrispende al massimo numero di ambienti che dovranno essere mantenuti aperti
contemporaneamente.
Nel nostro caso, l'altezza dell'albero di ricorsione risulta essere ![]() .
Pertanto, l'occupazione di memoria sarà
.
Pertanto, l'occupazione di memoria sarà
![]() .
.
Complemento 6+
Per questa particolare ricorrenza (
![]() ),
è possibile pensare ad un accorgimento
che consenta di ottenere un buon tempo di calcolo anche
per la procedura ricorsiva.
Sapresti indicare quale?
),
è possibile pensare ad un accorgimento
che consenta di ottenere un buon tempo di calcolo anche
per la procedura ricorsiva.
Sapresti indicare quale?
Svolgimento Complemento 6+
Si vede che la procedura può facilmente evitare di fare due chiamate ricorsive. Basta infatti sostituire, internamente alla procedura ricorsiva long long int T(int n), la riga di codice
return T(n-1) + T(n-1);
con la riga di codice
return 2*T(n-1);
così che la ricorrenza per il tempo di calcolo diviene
portando quindi ad un tempo di calcolo che sarà
![]() come è facile evidenziare srotolando la ricorrenza.
come è facile evidenziare srotolando la ricorrenza.
Purtroppo, tale modifica non migliora la situazione per quanto concerne l'occupazione di memoria.
Sapresti, come ulteriore esercizio,
modificare la versione iterativa di cui all'Esercizio 5,
ottenendo una soluzione algoritmica che richieda
solamente ![]() come occupazione di memoria,
senza per altro peggiorare il running time
(anzi, di fatto migliorando anche esso,
anche se non dal punto di vista asintotico)?
come occupazione di memoria,
senza per altro peggiorare il running time
(anzi, di fatto migliorando anche esso,
anche se non dal punto di vista asintotico)?