Esercizi di Preparazione

alla Prima Provetta

ASD1 2002-2003

Exercise 1   Allo scopo di tabulare la sequenza dei numeri di Fibonacci, come definiti dalla seguente ricorrenza

$$F_n = F_{n-1} + F_{n-2} \mbox{\hspace{1cm} per $n\geq 2$, con $F_0=0$\ e $F_1=1$}$$

Si consideri la seguente procedura iterativa.

#include<iostream.h>

int main() {
  int input_n; cout << "Dammi n: "; cin >> input_n; cout << endl;
  long long int F[input_n +1];   F[0] = 0;   F[1] = 1;
  for(int n=0; n<=1; n++)
    cout << "F[" << n << "] = "  << F[n] << endl;
  for(int n=2; n<=input_n; n++) {
    F[n] = F[n-1]+F[n-2];
    cout << "F[" << n << "] = "  << F[n] << endl;
  }
}

Si stabilisca l'ordine di crescita del tempo di calcolo della procedura proposta. Si stabilisca l'ordine di crescita della memoria impiegata dalla procedura proposta.

Exercise 2   Il professor Tortoise, propone di utilizzare la seguente procedura ricorsiva allo scopo di tabulare i numeri di Fibonacci.

#include<iostream.h>

long long int F(int n) {
  if(n==0) return 0;
  if(n==1) return 1;
  return F(n-1) + F(n-2);
}

int main() {
  int input_n; cout << "Dammi n: "; cin >> input_n; cout << endl;
  cout << "F[" << input_n << "] = "  << F(input_n) << endl;
}

Si stabilisca l'ordine asintotico di crescita per il tempo di calcolo della procedura proposta dal professor Tortoise. Si stabilisca l'ordine di crescita della memoria impiegata dalla procedura di Tortoise.

Exercise 3   La seguente procedura esemplifica come sia facile far sì che una procedura computi il numero di passi da essa stessa compiuto. Sapresti scrivere una ricorrenza che esprima il numero di passi della procedura? Credi di riuscire a risolvere tale ricorrenza, almeno asintoticamente?

#include<iostream.h>

long long int MyTime(int n) {
  int my_time = 1;
  while( (n/=2) > 0) my_time += MyTime(n) +1;
  return my_time;
}

int main() {
  int input_n; cout << "Dammi n: "; cin >> input_n; cout << endl;
  cout << "MyTime[" << input_n << "] = "  << MyTime(input_n) << endl;
}

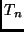
Exercise 4   Si determini l'andamento asintotico di un tempo di calcolo $T_n$ soggetto alla seguente ricorrenza

$$T(n) = \sum_{k+1}^{\lfloor \log_2 n \rfloor} T(\lfloor n/2^... ...heta(\log n) \mbox{\hspace{1cm} per $n \geq 1$, con $T(1)=1$}$$

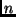
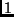
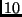
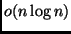
Exercise 5   Dare un'algoritmo che ordini una sequenza di $n$ numeri interi compresi tra $1$ e $10$ con complessità asintotica $o(n\log n)$. Quale è la complessità asintotica del tuo algoritmo? In che senso puoi concludere che il tuo algoritmo è ottimo?

Exercise 6   Dare un'algoritmo lineare che determini se in una sequenza di interi non negativi sia presente almeno una coppia di interi la cui somma valga 17. Qualora la sequenza in input fosse strettamente crescente, potresti migliorare la complessità asintotica?

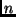
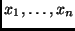
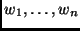
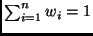
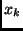
Exercise 7   Per $n$ elementi distinti $x_1, \ldots, x_n$ con pesi positivi $w_1, \ldots, w_n$ tali che $\sum_{i=1}^n w_i = 1$, il mediano pesato è l'elemento $x_k$ che soddisfa le seguenti diseguaglianze:

$$\sum_{x_i< x_k} w_i \leq \frac{1}{2}$$

e

$$\sum_{x_i> x_k} w_i \leq \frac{1}{2}.$$

Fornire un algoritmo che trovi il mediano pesato in tempo $\Theta(n)$.

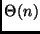
Aiuto: Se non sai da che parte partire, prova a porti prima degli obbiettivi più modesti, che ti consentano di familiarizzare con il problema, ad esempio:

• sapresti dimostrare l'esistenza del mediano pesato?
• sapresti fornire un algoritmo 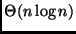$\Theta(n\log n)$ per la ricerca del mediano pesato?

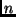
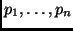
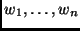
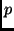
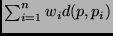
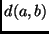
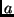
Exercise 8   Il Problema dell'Ufficio Postale è un problema di facility location definito come segue. Siano dati $n$ punti $p_1, \ldots, p_n$ con pesi associati $w_1, \ldots, w_n$. Si desidera trovare un punto $p$ (non necessariamente preso tra quelli in input) che minimizzi la somma $\sum_{i=1}^n w_i d(p,p_i)$, dove $d(a,b)$ è la distanza tra due punti $a$ e $b$.

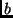
• Spiegare che il mediano pesato è un'ottima soluzione per il Problema dell'Ufficio Postale in una dimensione, in cui i punti sono numeri reali della retta reale e $d(a,b)=\vert a-b\vert$.
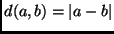• Trovare la soluzione per il Problema dell'Ufficio Postale in due dimensioni, dove i punti appartengano al piano ed ove si faccia riferimento alla distanza di Manhattan $d( (x_1,y_1), (x_2,y_2))=\vert x_1-x_2\vert + \vert y_1-y_2\vert$.
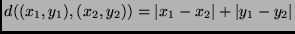• Sarebbe possibile generalizzare ad un numero arbitrario di dimensioni?