


Next: About this document ...
Correzione del facsimile C
Svolgimento Esercizio 1
- 1.
-
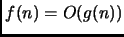 implica
implica
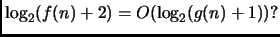
Vero. La dimostrazione formale, non richiesta,
sarebbe la seguente. Sappiamo che
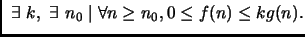 Sia
Sia
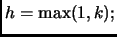 abbiamo
Siccome
abbiamo
Siccome 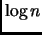 è una funzione crescente, otteniamo
Notiamo anche che
è una funzione crescente, otteniamo
Notiamo anche che
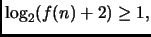 essendo
essendo
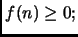 quindi la positività è assicurata per ogni
quindi la positività è assicurata per ogni
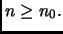
Essendo, per i medesimi valori di 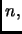 anche
anche
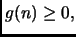 abbiamo
allo stesso modo
abbiamo
allo stesso modo
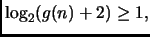 da cui
Essendo
da cui
Essendo 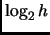 positivo, la costante trovata è certamente positiva.
positivo, la costante trovata è certamente positiva.
- 2.
-
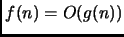 implica
implica
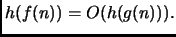
Falso, come si vede prendendo
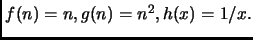 Ma risulta falso anche per
Ma risulta falso anche per
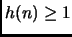 per ogni
per ogni 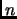 ,
come si vede prendendo
,
come si vede prendendo
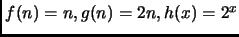 .
.
- 3.
-
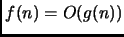 implica
implica
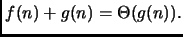
Vero. Abbiamo infatti che
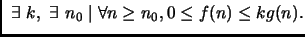 Quindi, sommando membro a membro
Quindi, sommando membro a membro 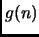 , otteniamo
, otteniamo
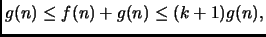 il che implica la tesi.
il che implica la tesi.
- 4.
-
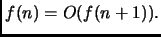
Falso, come si vede prendendo
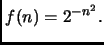 Detto infatti
Detto infatti
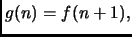 abbiamo
il cui limite è infinito, per cui
abbiamo
il cui limite è infinito, per cui
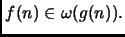 Se
Se 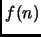 è non decrescente, la tesi è invece senz'altro vera.
è non decrescente, la tesi è invece senz'altro vera.
Esercizio 2
Siano
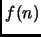
e
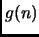
due funzioni definitivamente non negative.
Dimostrare che
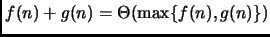
.
Svolgimento Esercizio 2
Sappiamo che
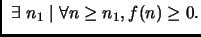 Analogamente,
sappiamo che
Analogamente,
sappiamo che
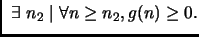 A partire
da
A partire
da
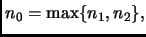 le due funzioni sono quindi entrambe non
negative. Per ogni
le due funzioni sono quindi entrambe non
negative. Per ogni 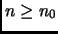 vale poi
vale poi
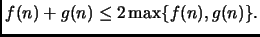 Riassumendo
Riassumendo
ove 
Esercizio 3
Ordinare le seguenti funzioni per ordine di crescita asintotico non
decrescente, ove
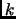
sia una costante positiva comune.
Ve ne sono alcune che presentano lo stesso ordine di crescita?
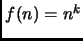
,
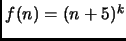
,
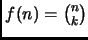
,
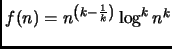
,
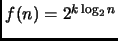
.
Svolgimento Esercizio 3
Abbiamo
Abbiamo dunque
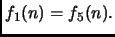 Inoltre,
Inoltre,
Segue poi
Infine, notando che
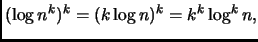 otteniamo
otteniamo
poiché abbiamo visto che una qualunque potenza positiva del logaritmo
cresce meno di una qualunque potenza positiva di 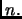 Ricordiamo
per completezza la dimostrazione di questo fatto: sia
Ricordiamo
per completezza la dimostrazione di questo fatto: sia
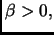 allora
allora
Se
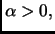 dove abbiamo usato il fatto che
dove abbiamo usato il fatto che
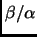 è pur sempre una
costante positiva cui si applica il fatto appena dimostrato.
In definitiva, come ordine di crescita abbiamo
è pur sempre una
costante positiva cui si applica il fatto appena dimostrato.
In definitiva, come ordine di crescita abbiamo
Esercizio 4
Si dimostri che
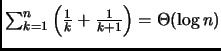
.
Svolgimento Esercizio 4
Sia
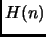 è detto ennesimo numero armonico.
Abbiamo
è detto ennesimo numero armonico.
Abbiamo
Per trovare un limite inferiore a 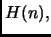 notiamo che
notiamo che
È consigliato farsi il disegno con l'''istogramma'' e la funzione che
lo approssima per capire meglio le manipolazioni effettuate. L'istogramma
viene poi buono anche per l'altra metà della dimostrazione.
Analogamente, infatti,
Quindi, avendo
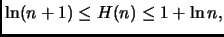 otteniamo
otteniamo
Essendo
otteniamo che
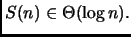 Notare che la base del logaritmo
diventa irrilevante nel passaggio alla notazione
Notare che la base del logaritmo
diventa irrilevante nel passaggio alla notazione 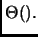
Approfondimento. La tesi
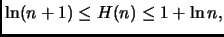 si può anche dimostrare per induzione - al solito, con un tantino
di senno di poi.
si può anche dimostrare per induzione - al solito, con un tantino
di senno di poi.
Per 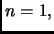 infatti, essa vale:
infatti, essa vale:
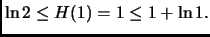
Supponendola vera per un certo 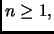 sommiamo membro a membro
sommiamo membro a membro
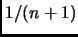 ad ottenere
ad ottenere
Se riuscissimo dunque a mostrare che, per ogni 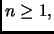
e
saremmo giunti alla tesi.
Le due richieste di sopra si possono riscrivere, effettuando anche uno
spostamento di indici nella prima, come segue:
I due fatti si possono dimostrare in un sol colpo ricordando il teorema
di Lagrange, per il quale data una funzione reale derivabile in
![$ [x, y],$](img116.png) ove
ove
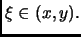 Nel nostro caso
ove
Nel nostro caso
ove
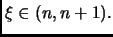 Da questo fatto le due tesi seguono immediatamente.
Da questo fatto le due tesi seguono immediatamente.
Si possono limitare i numeri armonici anche senza fare riferimento
al calcolo integrale. Sia
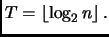 Notiamo che
Notiamo che
Trattiamo separatamente, per comodità, limite inferiore e superiore.
Per il primo, notiamo che
Analogamente, per il limite superiore,
Abbiamo cosí mostrato, con mezzi del tutto elementari, che
Esercizio 5
Dato un intero
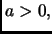
allo scopo di calcolare la potenza
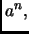
usiamo la seguente procedura
iterativa:
#include<iostream.h>
int main() {
int a; cout << "Dammi a: "; cin >> a; cout << endl;
int n; cout << "Dammi n: "; cin >> n; cout << endl;
long long int P[n +1];
P[0] = 1;
for(int k=1; k<=n; k++)
P[k] = a*P[k-1];
cout << "P[" << n << "] = " << P[n] << endl;
}
Si stabilisca l'ordine di crescita
del tempo di calcolo della procedura proposta.
Si stabilisca l'ordine di crescita
della memoria impiegata dalla procedura proposta.
Svolgimento Esercizio 5
La ricorrenza che calcola, ad esempio, il numero di moltiplicazioni, è:
che ha l'ovvia soluzione 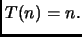
Per la memoria, siccome riserviamo per il calcolo di 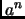 un array
di dimensione
un array
di dimensione 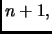 abbiamo
abbiamo
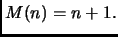
Esercizio 6
Il professor Gonzalez,
propone di utilizzare la seguente procedura
ricorsiva allo scopo di calcolare la medesima funzione:
#include<iostream.h>
long long int P(int a, int n) {
if (n==0) return 1;
if (n==1) return a;
return P(a, n/2)* P(a, n- (n/2));
}
int main() {
int a; cout << "Dammi a: "; cin >> a; cout << endl;
int n; cout << "Dammi n: "; cin >> n; cout << endl;
cout << "P[" << n << "] = " << P(a, n) << endl;
}
Si stabilisca l'ordine asintotico di crescita
per il tempo di calcolo della procedura
proposta dal professor Gonzalez.
Si stabilisca l'ordine di crescita
della memoria impiegata dalla procedura di Gonzalez.
Svolgimento Esercizio 6
Conoscendo come funziona la divisione intera del
C, vediamo che il procedimento
di calcolo adottato è il seguente:
A livello di moltiplicazioni abbiamo dunque
Ovviamente, possiamo applicare il Master Theorem ove 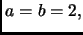
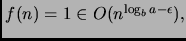 dove ad esempio
dove ad esempio
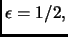 per ottenere
per ottenere
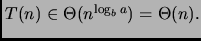 Chi, giustamente, non s'accontenta, cercherà di arrivare a una soluzione
precisa, data la facilità del caso. Procedendo a mano col seguente
programmino:
Chi, giustamente, non s'accontenta, cercherà di arrivare a una soluzione
precisa, data la facilità del caso. Procedendo a mano col seguente
programmino:
#include <iostream.h>
int T[10];
main() {
int i;
T[0]= T[1]= 0;
for (i=2; i<10; i++) {
T[i]= T[i/2] + T[i - i/2] + 1;
cout<<i<<" "<<T[i]<<endl;
}
}
constaterà che per 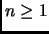 abbiamo
abbiamo
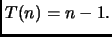 Proviamo a dimostrarlo per
induzione. Base,
Proviamo a dimostrarlo per
induzione. Base,
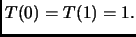 Serve trattare il caso
Serve trattare il caso 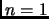 entro la base
poiché altrimenti otterremmo
entro la base
poiché altrimenti otterremmo
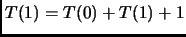 che non ha senso, non
da ultimo, perché descrive la ricorsione di un programma che non termina.
Usiamo dunque l'ipotesi induttiva
che non ha senso, non
da ultimo, perché descrive la ricorsione di un programma che non termina.
Usiamo dunque l'ipotesi induttiva
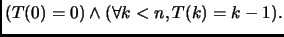 Abbiamo, per
Abbiamo, per 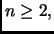
dove abbiamo usato nell'ordine: la relazione di ricorrenza; l'ipotesi
induttiva, ricordando che per 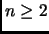 abbiamo sempre
abbiamo sempre
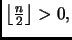 per cui ci possiamo
disinteressare al caso base
per cui ci possiamo
disinteressare al caso base 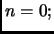 infine, il fatto che l'arrotondamento
superiore e quello inferiore della metà di un numero sommano al numero
stesso (distinguere i due casi pari e dispari per vederlo facilmente).
Abbiamo anche, ovviamente, sfruttato il fatto che per
infine, il fatto che l'arrotondamento
superiore e quello inferiore della metà di un numero sommano al numero
stesso (distinguere i due casi pari e dispari per vederlo facilmente).
Abbiamo anche, ovviamente, sfruttato il fatto che per
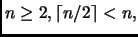 ed è quindi lecito applicarvi l'ipotesi induttiva.
La dimostrazione è quindi completa.
ed è quindi lecito applicarvi l'ipotesi induttiva.
La dimostrazione è quindi completa.
Per quanto riguarda la mamoria, notare che essa è proporzionale
al numero di attivazioni della procedura che coesistono sullo stack, il quale
a sua volta è al piú pari alla massimo numero di nodi su un ramo
dell'albero di ricorsione (radice e foglia comprese).
Tale distanza è governata dalla seguente ricorrenza:
Qui, ovviamente, gli uni stanno per unità di memoria consumate dalla singola
attivazione.
Per il Master theorem, con
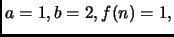 otteniamo che
otteniamo che
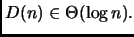 La soluzione esatta della ricorrenza è poi
stata ricavata in una delle precedenti raccolte di esercizi.
La soluzione esatta della ricorrenza è poi
stata ricavata in una delle precedenti raccolte di esercizi.
Notare che  ben diversamente dalla ricorrenza che esprime il tempo di
calcolo; questo è legato al fatto che, ad ogni istante, al piú
una attivazione di procedura chiamata consiste con l'attivazione
della procedura chiamante. Detto in altre parole, i comportamenti di
ben diversamente dalla ricorrenza che esprime il tempo di
calcolo; questo è legato al fatto che, ad ogni istante, al piú
una attivazione di procedura chiamata consiste con l'attivazione
della procedura chiamante. Detto in altre parole, i comportamenti di
 e di
e di 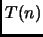 differiscono cosí profondamente perché
si può scrivere due volte nella stessa locazione di memoria,
ma non si può vivere due volte lo stesso istante...
differiscono cosí profondamente perché
si può scrivere due volte nella stessa locazione di memoria,
ma non si può vivere due volte lo stesso istante...
Complemento 6+
Dire come il prof. Gonzalez possa, con un semplice accorgimento,
ridurre il tempo di calcolo della sua procedura tanto da meritarsi
l'appellativo di Speedy. Quale è il nuovo tempo di calcolo?
Svolgimento Complemento 6+
Si vede che la procedura può facilmente evitare di fare due chiamate
ricorsive. Infatti, possiamo osservare che per 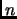 pari,
pari,
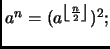 per
per 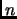 dispari,
dispari,
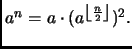 Questo suggerisce la
scrittura della seguente funzione:
Questo suggerisce la
scrittura della seguente funzione:
int power(int a, int n) {
int tmp;
if (n==0)
return 1;
if (n==1)
return a;
tmp= power(a, n/2);
return (n % 2) ? (a*(tmp*tmp)) : (tmp*tmp);
}
Applicando il Master Theorem ove
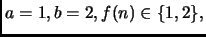 otteniamo
otteniamo
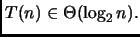
Approfondimento.
Qui, il computo esatto delle moltiplicazioni segue la legge
la cui tabulazione, e.g. con il programmino
main() {
int i;
T[0]= T[1]= 0;
for (i=2; i<20; i++) {
T[i]= (i%2) ? (T[i/2]+2) : (T[i/2]+1);
cout<<i<<" "<<T[i]<<endl;
}
}
dà i seguenti risultati:
n = 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
T(n)= 1 2 2 3 3 4 3 4 4 5 4 5 5 6 4
La decifrazione non è immediata come nei casi precedenti; ci si
rende conto che tuttavia 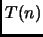 è legato al numero
è legato al numero 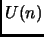 di uno che compaiono
nello sviluppo binario di
di uno che compaiono
nello sviluppo binario di 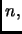 oltre che alla lunghezza
oltre che alla lunghezza 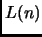 di
detto sviluppo. Nella procedura
di
detto sviluppo. Nella procedura 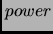 di sopra, infatti, la moltiplicazione
per
di sopra, infatti, la moltiplicazione
per 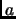 viene eseguita se e solo se
viene eseguita se e solo se 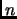 è dispari, ovvero, se la sua
cifra meno significativa è uno. Ricorsivamente, ci interesseremo poi
alla parità di
è dispari, ovvero, se la sua
cifra meno significativa è uno. Ricorsivamente, ci interesseremo poi
alla parità di
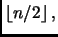 e via dicendo.
La cosa piú naturale è cercare una formuletta del tipo
Scegliamo tre valori a caso, e.g.
e via dicendo.
La cosa piú naturale è cercare una formuletta del tipo
Scegliamo tre valori a caso, e.g. 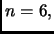
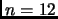 e
e 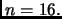 Lo sviluppo di
Lo sviluppo di 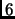 è
è 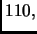 quello di
quello di 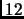 è
è
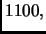 quello di 16 è
quello di 16 è 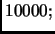 vogliamo quindi
da cui
vogliamo quindi
da cui
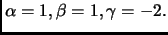 Proviamo a vedere se la formula funziona:
Proviamo a vedere se la formula funziona:
n L(n) U(n) L(n)+U(n)-2
0 1 0 -1
1 1 1 0
2 2 1 1
3 2 2 2
4 3 1 2
5 3 2 3
6 3 2 3
7 3 3 4
8 4 1 3
Sembra che per 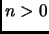 funzioni. Dimostriamolo dunque per induzione.
Innanzitutto,
funzioni. Dimostriamolo dunque per induzione.
Innanzitutto,
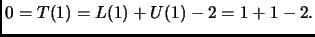 Supponiamo che per
Supponiamo che per
![$ k \in [1, n-1]$](img205.png) sia
sia
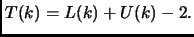 Sia
Sia  pari. Allora
pari. Allora 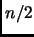 ha un bit in meno, e lo stesso numero di uni.
ha un bit in meno, e lo stesso numero di uni.
Abbiamo
Sia 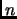 dispari. Allora
dispari. Allora
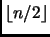 ha un bit in meno, e anche un uno in meno.
ha un bit in meno, e anche un uno in meno.
Abbiamo
La dimostrazione è dunque completa. Sappiamo poi che, per 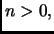
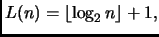 e che ovviamente
e che ovviamente
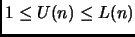 (casi estremi: solo la cifra piú significativa dello sviluppo
è uno, oppure tutte le cifre sono uno). Abbiamo quindi
dove il limite inferiore è toccato quando
(casi estremi: solo la cifra piú significativa dello sviluppo
è uno, oppure tutte le cifre sono uno). Abbiamo quindi
dove il limite inferiore è toccato quando 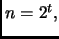 quello superiore
quando
quello superiore
quando
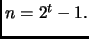



Next: About this document ...
Romeo Rizzi
2002-10-22
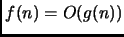 implica
implica
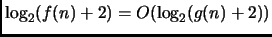 .
.
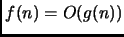 implica
implica
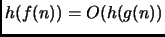 .
.
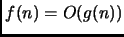 implica
implica
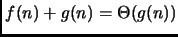 .
.
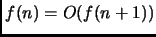 .
.
![]() Quindi, sommando membro a membro
Quindi, sommando membro a membro ![]() , otteniamo
, otteniamo
![]() il che implica la tesi.
il che implica la tesi.
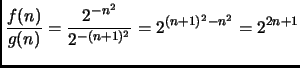
![]() Analogamente,
sappiamo che
Analogamente,
sappiamo che
![]() A partire
da
A partire
da
![]() le due funzioni sono quindi entrambe non
negative. Per ogni
le due funzioni sono quindi entrambe non
negative. Per ogni ![]() vale poi
vale poi
![]() Riassumendo
Riassumendo
![]() Inoltre,
Inoltre,
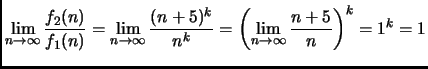
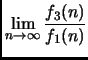
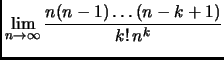
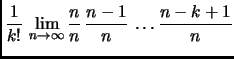
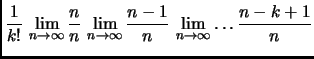
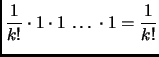
![]() otteniamo
otteniamo
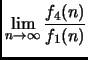
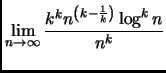
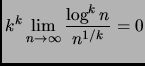
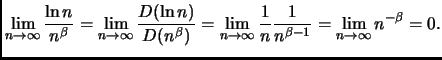
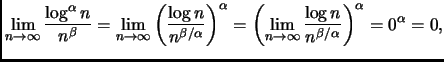
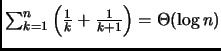 .
.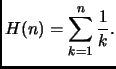
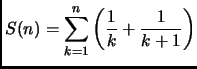
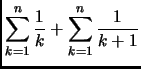
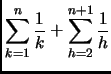
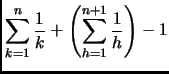
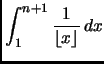
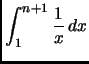
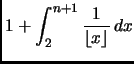
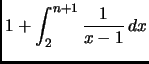
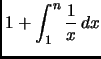
![]() otteniamo
otteniamo
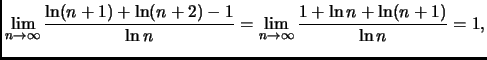
![]() si può anche dimostrare per induzione - al solito, con un tantino
di senno di poi.
si può anche dimostrare per induzione - al solito, con un tantino
di senno di poi.
![]() infatti, essa vale:
infatti, essa vale:
![]()
![]() sommiamo membro a membro
sommiamo membro a membro
![]() ad ottenere
ad ottenere
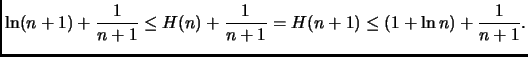
![]()
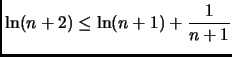
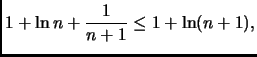
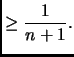
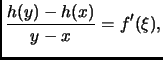
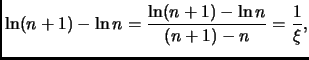
![]() Notiamo che
Notiamo che
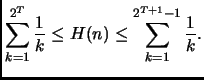
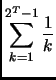
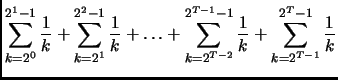
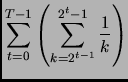
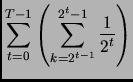
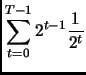
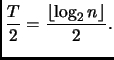
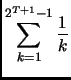
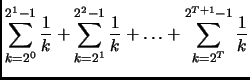
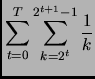
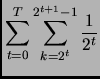
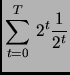
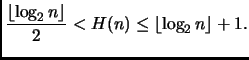
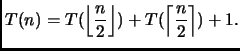
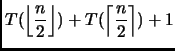
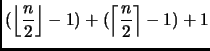
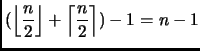
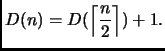
![]() pari,
pari,
![]() per
per ![]() dispari,
dispari,
![]() Questo suggerisce la
scrittura della seguente funzione:
Questo suggerisce la
scrittura della seguente funzione: