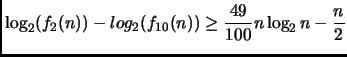Riscriviamole intanto nei modi più convenienti per il confronto. Di
quasi tutte diamo anche il logaritmo in base due, poichè per ordinare
molte di esse è sufficiente confrontarne i logaritmi.
Sia infatti
![]() e
e
![]() Abbiamo allora i fatti seguenti:
Abbiamo allora i fatti seguenti:
Dimostriamo a): se
![]() allora
allora
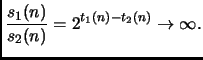
Per dimostrare b), notiamo che
![]() è
equivalente a dire
è
equivalente a dire
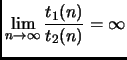
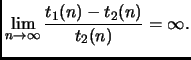
Veniamo alle dieci funzioni. Per i fattoriali, sfruttiamo il fatto
che
![]()
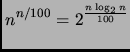 |
Le due funzioni con logaritmo minore sono ![]() e
e ![]() chiaramente,
chiaramente,
![]() Usiamo la notazione del confronto fra
numeri seguendo l'ovvia analogia.
Subito dopo vengono
Usiamo la notazione del confronto fra
numeri seguendo l'ovvia analogia.
Subito dopo vengono ![]() e
e ![]() Seguono le
funzioni che hanno logaritmo lineare; vediamo che
Seguono le
funzioni che hanno logaritmo lineare; vediamo che
![]() Vi sono poi tre funzioni il coi logaritmo è
Vi sono poi tre funzioni il coi logaritmo è
![]() Se è chiaro che
Se è chiaro che
![]() bisogna classificare
bisogna classificare
![]() Mostriamo che essa cresce meno del fattoriale.
Ricordiamo che
Mostriamo che essa cresce meno del fattoriale.
Ricordiamo che
![]() da cui
da cui