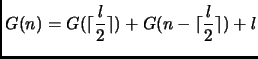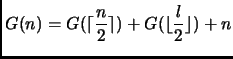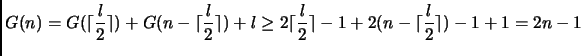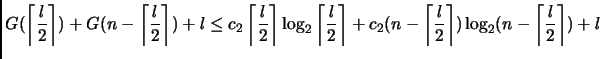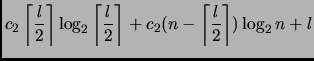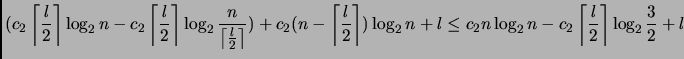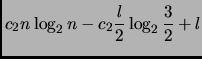Input: un sacchetto di cioccolatini.
1. se il sacchetto contiene al più un cioccolatino,
allora mangiatelo e termina.
2. prendi un cioccolatino dal sacchetto ricevuto
in input, leccalo, e mettilo in un sacchetto
di cioccolatini leccati.
3. se il sacchetto ricevuto in input
non è ancora vuoto,
e finchè non ti assale lo scrupolo per
il fatto di essere in dieta, puoi ripetere il passo 2.
4. preso dallo scrupolo (o dai rimpianti),
conta i cioccolatini leccati,
siano essi ![]() .
.
5. nel tentativo di nascondere la tua debolezza,
sposta
![]() cioccolatini
dal sacchetto dei leccati al sacchetto ricevuto in input.
cioccolatini
dal sacchetto dei leccati al sacchetto ricevuto in input.
6. agisci da Goloson
sul sacchetto dei cioccolatini leccati.
7. agisci da Goloson
sul sacchetto dei cioccolatini ricevuto in input.
Sia ![]() il numero massimo di degustazioni di cioccolatino
(leccatine + magnate) in cui si può incorrere partendo da
un sacchetto di
il numero massimo di degustazioni di cioccolatino
(leccatine + magnate) in cui si può incorrere partendo da
un sacchetto di ![]() cioccolatini.
Descrivere
cioccolatini.
Descrivere ![]() tramite una ricorrenza.
Condurre analisi asintotica per
tramite una ricorrenza.
Condurre analisi asintotica per ![]() .
Riesci ad estrapolare od intuire la politica da tenere
(quando conviene farsi prendere da scrupolo)
qualora si voglia massimizzare il numero di degustazioni?
Quale potrà essere invece il
minor numero di degustazioni possibili partendo
da un sacchetto di
.
Riesci ad estrapolare od intuire la politica da tenere
(quando conviene farsi prendere da scrupolo)
qualora si voglia massimizzare il numero di degustazioni?
Quale potrà essere invece il
minor numero di degustazioni possibili partendo
da un sacchetto di ![]() cioccolatini?
Riesci ad estrapolare anche formalmente quale politica porti
a questo minimo.
cioccolatini?
Riesci ad estrapolare anche formalmente quale politica porti
a questo minimo.