Visto che ![]() deve essere pari, possiamo scrivere direttamente
deve essere pari, possiamo scrivere direttamente
![]()
Prima soluzione: abbiamo
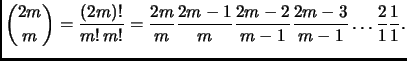
Seconda soluzione. Secondo la formula di Stirling
![$ k! = [1+ \Theta(k^{-1})] \sqrt{2 \pi k} \left( \frac{k}{e} \right)^k $](img150.png) da cui
da cui
![$\displaystyle {2m \choose m} = \frac{(2m)!}{m! m!} =[1+ \Theta(m^{-1})]
\sqrt{\frac{1}{\pi m}} 2^{2m}. $](img151.png)
Terza soluzione: i coefficienti della riga ![]() -esima del triangolo di
Tartaglia sommano a
-esima del triangolo di
Tartaglia sommano a ![]()
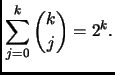
Tra l'altro, ricordiamo che
![]() è il più grande dei
coefficienti della riga
è il più grande dei
coefficienti della riga ![]() -esima, in quanto i coefficienti binomiali
crescono muovendosi dai lati verso il centro. Questo si può vedere
facilmente scrivendo
-esima, in quanto i coefficienti binomiali
crescono muovendosi dai lati verso il centro. Questo si può vedere
facilmente scrivendo
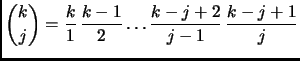
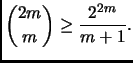
![]() Il risultato che si ottiene con Stirling,
Il risultato che si ottiene con Stirling,
![]() ci dice che la verità
sta proprio nel mezzo.
ci dice che la verità
sta proprio nel mezzo.