La difficoltà sta nella presenza dell'arrotondamento superiore, visto che stiamo calcolando un limite superiore.
Per avere una idea qualitativa, partiamo dal caso ![]() in modo da
non avere problemi di arrotondamento.
Se poniamo ad esempio
in modo da
non avere problemi di arrotondamento.
Se poniamo ad esempio ![]() la soluzione esatta è:
la soluzione esatta è:
Sulle potenze di due, dunque,
![]() Questo suggerisce
di tentare, nel caso generale, una ipotesi induttiva della forma
Questo suggerisce
di tentare, nel caso generale, una ipotesi induttiva della forma
![]() Del termine
Del termine ![]() si vede la necessità nel caso base, in quanto
vogliamo che
si vede la necessità nel caso base, in quanto
vogliamo che
![]() Questo fornisce il vincolo
Questo fornisce il vincolo
![]() Per quanto riguarda il passo induttivo, sfruttando l'ipotesi
induttiva otteniamo
Per quanto riguarda il passo induttivo, sfruttando l'ipotesi
induttiva otteniamo
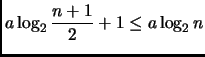
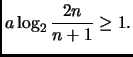
Sappiamo che ![]() ha un comportamento logaritmico, dobbiamo però
trovarne la forma esatta.
Conviene tabulare qualche valore:
ha un comportamento logaritmico, dobbiamo però
trovarne la forma esatta.
Conviene tabulare qualche valore:
n T(n) 1 1 2 2 3 2 4 3 5 3 6 3 7 3 8 4
La funzione cambia in corrispondenza delle potenze di due, quindi
fa certamente riferimento a
![]() Se facesse riferimento a
Se facesse riferimento a
![]() scatterebbe infatti in
corrispondenza delle potenze di due aumentate di uno.
scatterebbe infatti in
corrispondenza delle potenze di due aumentate di uno.
Si vede facilmente che
![]() si tratta
di dimostrarlo per induzione.
si tratta
di dimostrarlo per induzione.
Base:
![]() nessun problema.
nessun problema.
Passo induttivo: dobbiamo mostrare che
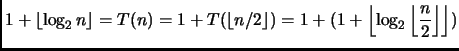
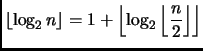
Meglio cambiare punto di vista: anziché esprimere ![]() in funzione
di
in funzione
di ![]() proviamo a
fare l'inverso, esprimendo
proviamo a
fare l'inverso, esprimendo ![]() in funzione di
in funzione di ![]() Siccome
Siccome
![]() non è iniettiva,
non è iniettiva,
![]() è un insieme.
Guardando ai valori tabulati, si capisce subito quale:
è un insieme.
Guardando ai valori tabulati, si capisce subito quale:
![$\displaystyle \left\lfloor \frac{n}{2} \right\rfloor \in [2^{T(\left\lfloor \frac{n}{2} \right\rfloor )-1},
2^{T(\left\lfloor \frac{n}{2} \right\rfloor )} -1].$](img46.png)
Ora, dalla proprietà dimostrata per induzione e dalla definizione di logaritmo segue la forma chiusa che avevamo intuito.
n T(n) S(n) 1 1 1 2 2 2 3 2 3 4 3 3 5 3 4 6 3 4 7 3 4 8 4 4 9 4 5È facile notare che per
Dimostriamolo per induzione, partendo dalla base ![]()
![]() infatti lo possiamo calcolare a mano, verificando direttamente
che
infatti lo possiamo calcolare a mano, verificando direttamente
che
![]()
Per il passo induttivo,
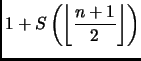 |
|||
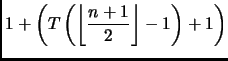 |
|||
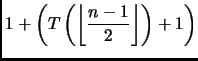 |
|||
Nell'algoritmo mergesort, abbiamo
![]() e
e
![]() (o viceversa),
da cui il numero di confronti sta nell'intervallo
(o viceversa),
da cui il numero di confronti sta nell'intervallo
![]()
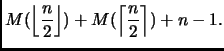 |
| 0 | |||
Veniamo al caso generale. Come curiosità, consideriamo anche la ricorrenza relativa al caso migliore, quello in cui ogni operazione di merge esaurisce nel modo piú rapido possibile la lista più corta:
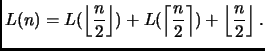
Con una semplice procedura
void table_mergesort()
{
int i;
M[1]= 0;
cout<<" n L(n) M(n) M(n)-M(n-1)"<<endl<<endl;
for (i=2; i<18; i++)
M[i]= M[i/2] + M[(i+1)/2] + i - 1;
for (i=2; i<18; i++)
L[i]= L[i/2] + L[(i+1)/2] + i/2;
for (i=1; i<18; i++) {
cout<<" "<<i<<" "<<L[i]<<" "<<M[i];
if (i>1)
cout<<" "<<M[i]-M[i-1];
cout<<endl;
}
}
possiamo tabulare i primi valori di tali ricorrenze, dove di
n L(n) M(n) M(n)-M(n-1)
1 0 0
2 1 1 1
3 2 3 2
4 4 5 2
5 5 8 3
6 7 11 3
7 9 14 3
8 12 17 3
9 13 21 4
10 15 25 4
11 17 29 4
12 20 33 4
13 22 37 4
14 25 41 4
15 28 45 4
16 32 49 4
17 33 54 5
Si nota che, detto
![]() , abbiamo
, abbiamo
![]() Verifichiamolo, trovando una
ricorrenza per
Verifichiamolo, trovando una
ricorrenza per ![]()
![$\displaystyle M(\left\lfloor \frac{n}{2} \right\rfloor ) + M(\left\lceil \frac{...
...rac{n-1}{2} \right\rfloor ) + M(\left\lceil \frac{n-1}{2} \right\rceil ) + n-2]$](img107.png) |
|||
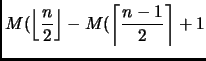 |
|||
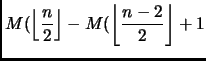 |
|||
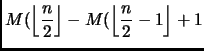 |
|||
 |
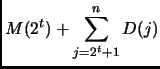 |
|||
 |
|||