


Next: About this document ...
Fac Simile di Scritto (A)
ASD1 2002-2003
Exercise 2
Dimostrare che
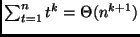
,
per ogni numero naturale
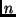
.
Exercise 3
Ordinare le seguenti funzioni per ordine di crescita asintotico non
decrescente, ove
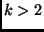
sia una costante positiva comune.
Ve ne sono alcune che presentano lo stesso ordine di crescita?
Come cambia la situazione per
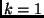
?
E cosa succede per
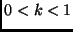
?
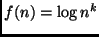
,
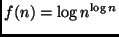
,
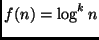
,
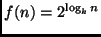
.
Exercise 4
Un grafo di dice
Euleriano
se è connesso ed ogni nodo ha grado pari.
Un cammino che parta da un nodo
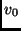
,
attraversi tutti gli archi una ed una sola volta
(possibilmente ripassando per uno stesso nodo più di una volta),
ritornando infine in
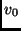
,
è detto un
cammino Euleriano.
- Dimostrare che un grafo
ammette un cammino Euleriano se e solo se è Euleriano.
- Descrivere un algoritmo con tempo di calcolo
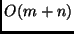 (ossia lineare)
che dato in input un grafo Euleriano
(ossia lineare)
che dato in input un grafo Euleriano 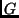 restituisca un cammino Euleriano in
restituisca un cammino Euleriano in 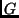 .
.
Exercise 5
Si consideri il seguente algoritmo di Trémaux.
- 1.
- mi risveglio in una stanza di un labirinto ignoto;
- 2.
- finchè vi è un cunicolo che esca dalla stanza in cui mi trovo
ed il cui imbocco non sia stato ancora marcato
- 3.
- scelgo uno dei cunicoli non marcati,
ne marco l'imbocco con una croce, e lo attraverso;
- 4.
- come giungo nella stanza all'altra estremità del cunicolo,
se mi ritrovo in una nuova stanza,
allora marco l'imbocco che mi ha ivi condotto con una 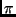 ;
;
altrimenti, lo marco con una croce, e ripercorro il cunicolo a ritroso;
- 5.
- se nella stanza in cui mi trovo vi è un cunicolo marcato con
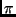 ,
,
allora attraverso tale cunicolo e vado al Passo 2;
- 6.
- altrimenti, la mia esplorazione è finita.
Dimostrare che ogni arco viene attraversato,
nella stessa direzione, al più una volta.
Se ne deduca un upper bound sul tempo di calcolo.
Si dimostri che se il grafo è connesso allora
ogni arco viene attraversato precisamente una volta
in entrambe le direzioni.



Next: About this document ...
Romeo Rizzi
2002-11-14
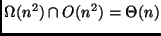 .
.
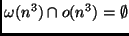 .
.
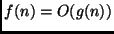 implica
implica
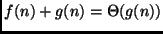 .
.
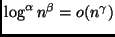 per ogni
per ogni
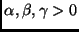 .
.