Notazione Asintotica
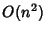 ,
,
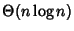 ,
, 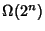 ,
, 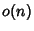 ,
, 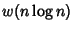
Definition 1
Diremo che una funzione
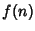
appartiene a
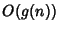
(ma chissà poi perchè si è soliti scrivere
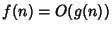
invece di
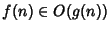
)
quando
esistono delle costanti positive
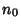
e
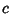
tali che
Definition 2
Diremo che una funzione
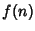
appartiene a
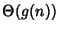
(ma poi si è soliti scrivere
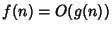
invece di
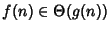
)
quando
esistono delle costanti positive
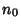
,
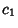
e
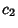
tali che
Definition 3
Diremo che una funzione
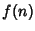
appartiene a
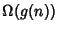
(ma poi si è soliti scrivere
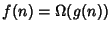
invece di
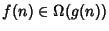
)
quando
esistono delle costanti positive
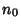
e
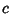
tali che
Exercise 1
Dimostare che
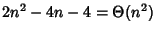
.
Dimostare che
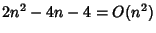
.
Exercise 2
È vero o falso che
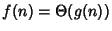
implica che
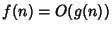
? Argomentarlo.
È vera anche l'implicazione inversa?
Fornire un controesempio.
Exercise 3
È vero o falso che
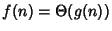
implica che
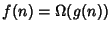
? Argomentarlo.
È vera anche l'implicazione inversa?
Fornire un controesempio.
Exercise 4
Dimostrare che
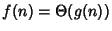
se e solo se abbiamo sia che
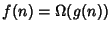
ma anche che
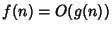
.
Exercise 5
Dimostrare che
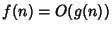
se e solo
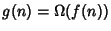
.
Possiamo ora concludere, tramite l'esercizio precedente, che
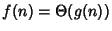
se e solo se
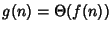
?
Definition 4
Scriveremo
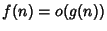
quando per una qualunque costante
positiva
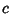
, esiste una costante positiva
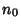
tale che
Definition 5
Scriveremo
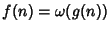
quando per una qualunque costante
positiva
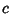
, esiste una costante positiva
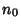
tale che
Exercise 6
È vero o falso che
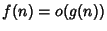
implica
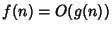
?
È vera anche l'implicazione inversa?
Fornire un controesempio.
Exercise 7
È vero o falso che
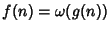
implica
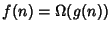
?
È vera anche l'implicazione inversa?
Fornire un controesempio.
Exercise 8
Dimostrare che
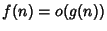
se e solo
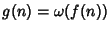
.
Exercise 9
Si supponga di definire
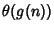
come l'insieme di quelle funzioni
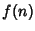
tali che
sia
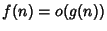
che
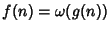
valgano.
Come mai siamo sicuramente dei pionieri nel proporre questa nuova
classe di funzioni?
Exercise 11
Ordinare le seguenti funzioni per ordine di crescita asintotico non
decrescente. Ve ne sono alcune che presentano lo stesso ordine di crescita?
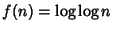
,
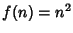
,
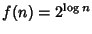
,
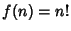
,
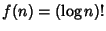
,
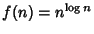
,
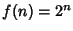
,
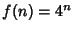
,
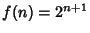
,
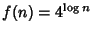
,
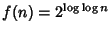
,
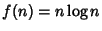
,
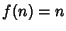
,
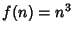
,
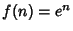
,
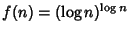
,
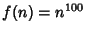
,
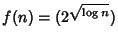
,
Exercise 12
Siano
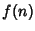
e
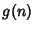
due funzioni asintoticamente non negative.
Dimostrare che
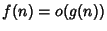
se e solo se
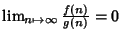
.
Exercise 13
Siano
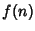
e
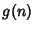
due funzioni asintoticamente non negative.
Si assuma che
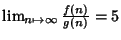
.
Dimostrare che
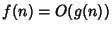
.
Possiamo concludere che
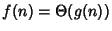
?
Exercise 14
Stirling riuscí finalmente a coronare
i propri sforzi per l'approssimazione
asintotica di
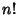
producendo la seguente formula.
Si utilizzi la formula di Stirling
per dimostrare che
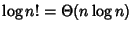
.
Ottenere lo stesso risultato senza avvalersi della
formula di Stirling.
Possiamo concludere qualcosa sul minor numero di confronti
necessario per l'ordinamento di
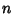
numeri?
|
2002-09-30
|
© Dipartimento di Matematica ed Informatica - Università di Udine
|