F-formation discovery in static images
|
Detection of groups of interacting people is a very interesting and useful task in many modern technologies, with application fields spanning from video-surveillance to social robotics. In this page we collect all the work on this topics performed at the University of Verona by the VIPS Lab members. Two alternative strategies have been proposed over the last years: one based on Hough-Voting and one on Graph-Cuts. All the code and data in this page are freely usable for any scientific research purpose, but if you do that, please cite the related papers. We strongly recommend the reading of the paper "F-formation Detection: Individuating Free-standing Conversational Groups in Images" for a rigorous definition of group considering the background of the social sciences, which allows us to specify many kinds of group, so far neglected in the Computer Vision literature. On top of this taxonomy, a detailed state of the art on the group detection algorithms is presented in the paper. |

|
|
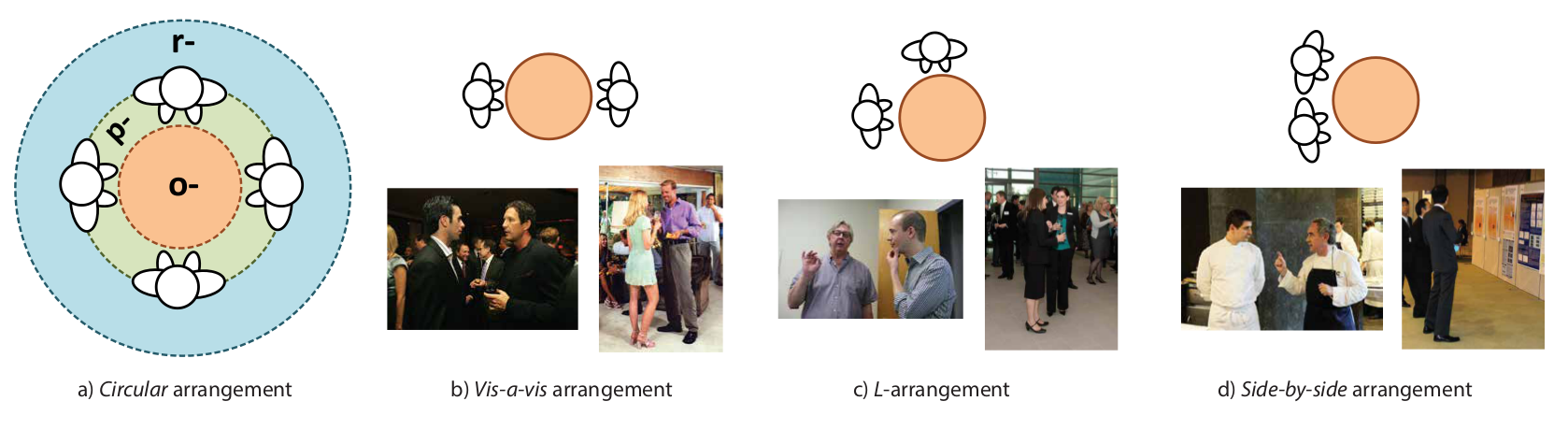
In practice, an F-formation is the proper organization of three social spaces: o-space, p-space and r-space. The o-space is a convex empty space surrounded by the people involved in a social interaction, where every participant looks inward into it, and no external people is allowed in this region. The p-space is a narrow stripe that surrounds the o-space, and that contains the bodies of the participants, while the r-space is the area beyond the p-space. There can be different configurations for F-formations; in the case of two participants, typical F-formation arrangements are vis-a-vis, L-shape, and side-by-side. When there are more than three participants, a circular formation is typically formed. |
Methods
|
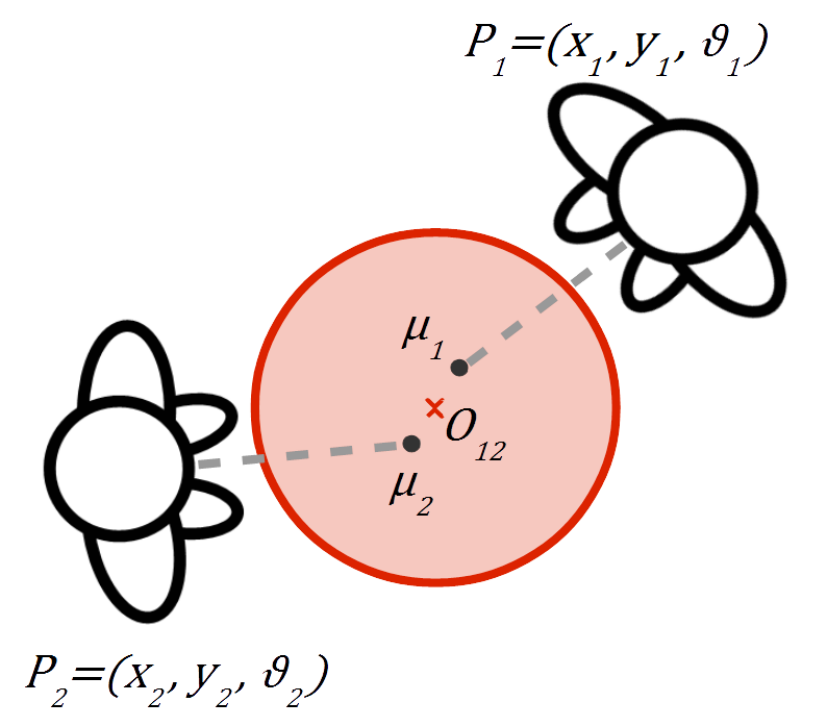
Suppose to know the position and orientation of each individual i in the scene . The goal is to find the o-space where j are the indexes of all the individuals belonging to it (see figure). Sociologists introduced the concept transactional segment of an individual as "the area in front of him/her that can be reached easily, and where hearing and sight are most effective" [Ciolek, 1983]. We model the transactional segment of the individual i with a gaussian distribution , where and . Variables and are input parameters for both HVFF and GCFF algorithms. This formulation has to handle with the visibility constraint which prevent a person to be assigned to a specific group if another individual is occluding him the o-space. To cluster the transactional segments of the individuals in the scene, we developed over the years several versions of two main methodologies described below. For more details on the algorithms, please refer to the papers. |
|
Hough Voting for F-Formations (HVFF)
Under this caption, we consider a set of methods based on a Hough-Voting strategy to build accumulation spaces and find local maxima of this function. The general idea is that each Gaussian probability density function representing the transactional segment of an individual can be approximated by a set of samples, which basically vote for a given o-space centre location. The voting space is then quantized and the votes are aggregated on squared cells, so to form a discrete accumulation space. Local maxima in this space identify o-space centres, and consequently, F-formations. In all these methods the visibility constraint is applied afterwards by checking the composition of the group and its geometry
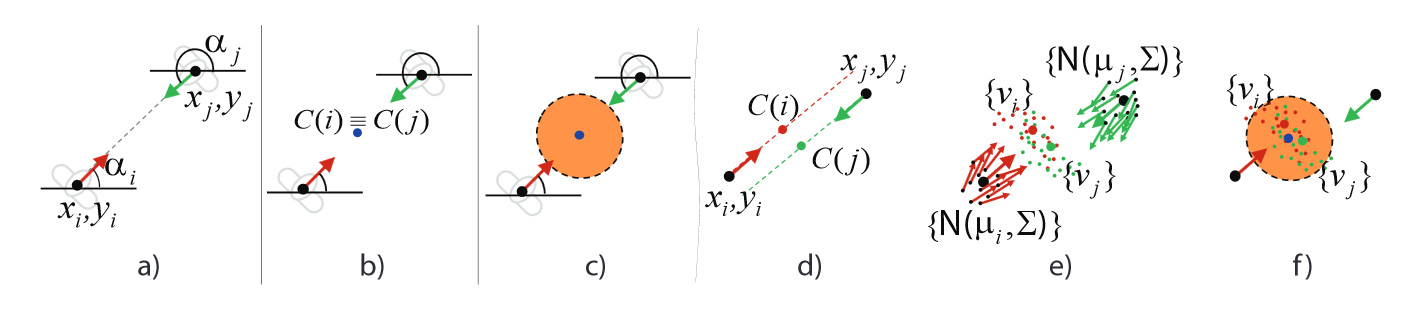
(a-c) Two subjects exactly facing each other at a fixed distance vote for the same centre of the circumference representing the o-space. (d) The 2 subjects do not face each other exactly in real cases. (e-f) Several positions and head orientations are drawn from Gaussian distributions associated to the subjects so as to deal with the uncertainty of real scenarios, robustifying the proposed approach. |
The first work in this field has been presented at BMVC 2011 [1]; in this paper the votes are linearly accumulated by just summing up all the weights of votes belonging to the same cell. A first improvement of this approach has been presented at WIAMIS 2013 [2], where the votes are aggregated by using the weighted Boltzmann entropy function. In the same year, at ICIP 2013 [3], a multi-scale approach is used on top of the entropic version: the idea is that groups with higher cardinality tends to arrange around a larger o-space; the entropic group search runs for different o-space dimensions by filtering groups cardinalities; afterwards, a fusion step is based on a majority criterion. |
Graph-Cuts for F-Formation (GCFF)
With this method we propose to use the power of graph-cuts algorithms in clustering graphs, while we need to build a good description of the scene in form of graph. In our formulation the nodes are represented by individuals (i.e. the transactional segments of individuals) and the candidate o-space centres, while edges are defined between each pair of nodes of different type (i.e. between a transactional segment and a candidate o-space centre). We model the probability of each individual to belong to a specific o-space as: . We then build the cost function by adding a Minimum Description Length (MDL) prior and considering the log function of the probability obtained. Moreover, we introduce an additive term which acts as the visibility constraint on the individual i regardless of the group person j is assigned to. The final objective function becomes:
Code
The code for both HVFF and GCFF is publicly available under the GPL license. Everyone can use this code for research purposes. If you publish results of the research, please cite the related papers as reported in the README.txt file inside the zip folder.
Datasets
Several datasets for group detection in still images have been released recently. We tested the code in this page over the following datasets that can be downloaded from the linked webpages. Anyway, a compact version of the datasets useful for running the code is also provided here: download.
| Dataset | Data Type | Detections | Detection Quality |
|---|---|---|---|
| Synthetic Data | synthetic | -- | perfect |
| IDIAP Poster Data | real | manual | very high |
| Cocktail Party Data | real | automatic | high |
| Coffee Break Data | real | automatic | low |
| GDet Data | real | automatic | very low |
- Synthetic Data (link): a psychologist generated a set of 10 diverse situations, each one repeated with minor variations for 10 times, resulting in 100 frames representing different social situations, with the aim to span as many confiurations as possible for F-formations. An average of 9 individuals and 3 groups are present in the scene, while there are also individuals not belonging to any group. Proxemic information is noiseless in the sense that there is no clutter in the position and orientation state of each individual.
- IDIAP Poster Data (link): over 3 hours of aerial videos (654x439px) recorded during a poster session of a scientific meeting. Over 50 people are walking through the scene, forming several groups over time. A total of 24 annotators were grouped into 3-person subgroups and they were asked to identify F-formations and their associates from static images, for a total of 82 frames. Each person's position and body orientation was manually labelled and recorded as pixel values in the image plane {one pixel represented approximately 1.5cm).
- Cocktail Party Data (email): this dataset contains about 30 minutes of video recordings of a cocktail party in a 30m2 lab environment involving 7 subjects. The party was recorded using four synchronised angled-view cameras (15Hz, 1024x768px, jpeg) installed in the corners of the room. Subject's positions and head pose estimation were logged using a particle filter-based body tracker specifically designed by the dataset's owners. Groups in one frame every 5 seconds were manually annotated by an expert, resulting in a total of 320 labelled frames for evaluation. In this dataset proxemic information is estimated automatically, so errors may be present; anyway, due to the highly supervised scenario, errors are very few.
- Coffee Break Data (link): the dataset focuses on a coffee-break scenario of a social event, with a maximum of 14 individuals organised in groups of 2 or 3 people each. Images are taken from a single camera (1440x1080px). People positions have been estimated by exploiting multi-object tracking on the heads, and head detection has been performed afterwards, considering solely 4 possible orientations (front, back, left and right) in the image plane, and then projected onto the ground plane. A psychologist annotated the videos indicating the groups present in the scenes, for a total of 119 frames. The annotations were generated by analysing each frame in combination with questionnaires that the subjects filled in. This dataset represent one of the most difficult benchmark, since the rough head orientation information, also affected by noise, gives in many cases unreliable information. Anyway, it represents also one of the most realistic scenario, since all the proxemic information comes from automatic, off-the-shelf, computer vision tools.
- GDet Data (link): the dataset is composed by 5 subsequences of images acquired by 2 angled-view low resolution cameras (352x328px) with a number of frames spanning from 17 to 132, for a total of 403 annotated frames. The scenario is a vending machines area where people meet and chat while they are having coffee. This is similar to Coffee Break scenario but in this case the scenario is indoor, which makes occlusions many and severe; moreover, people in this scenario knows each other in advance. The videos were acquired with two monocular cameras, located on opposite angles of the room. To ensure the natural behaviour of people involved, they were not aware of the experiment purposes. Ground truth generations follows the same protocol as in Coffee Break; but in this case people tracking has been performed using a particle filter approach. Also in this case, head orientation was fixed to 4 angles. This dataset, together with Coffee Break, is the closest to what computer vision can give as input to our group detection technique.
References
- Social interaction discovery by statistical analysis of F-formations
Cristani M., Bazzani L., Paggetti G., Fossati A., Tosato D., Del Bue A., Menegaz G., Murino V.
22nd British Machine Vision Conference (BMVC 2011), Dundee, UK, 2011
[PDF] [BibTex] [web]
- Group Detection in Still Images by F-formation Modeling: a Comparative Study
Setti F., Hung H., Cristani M.
14th International Workshop on Image and Audio Analysis for Multimedia Interactive Services (WIAMIS 2013), Paris, France, 2013
[PDF] [BibTex] [web]
- Multi-scale F-formation discovery for group detection
Setti F., Lanz O., Ferrario R., Murino V., Cristani M.
IEEE International Conference on Image Processing (ICIP 2013), Melbourne, Australia, 2013
[PDF] [BibTex] [web]
- F-formation Detection: Individuating Free-standing Conversational Groups in Images Setti F., Russell C., Bassetti C. and Cristani M. preprint on arXiv.org [PDF] [BibTex] [web]

|

|